题目内容
9.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,1),则$\overrightarrow{a}$+2$\overrightarrow{b}$=( )| A. | (0,5) | B. | (5,-1) | C. | (-1,3) | D. | (-3,4) |
分析 直接利用向量的坐标运算求解即可.
解答 解:向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-2,1),
则$\overrightarrow{a}$+2$\overrightarrow{b}$=(1,2)+2(-2,1)=(-3,4).
故选:D.
点评 本题考查向量的坐标运算,考查计算能力,会考常考题型.

练习册系列答案
相关题目
19.圆x2+y2=1在伸缩变换$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$的作用下,所得方程是( )
| A. | 4x′2+9y′2=1 | B. | $\frac{{{{x'}^2}}}{2}+\frac{{{{y'}^2}}}{3}=1$ | C. | $\frac{{{{x'}^2}}}{9}+\frac{{{{y'}^2}}}{4}=1$ | D. | $\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$ |
17.已知向量$\overrightarrow{OA}$=(2,2),$\overrightarrow{OB}$=(4,1),在x轴上有一点P,使$\overrightarrow{AP}$•$\overrightarrow{BP}$有最小值,则P点坐标为( )
| A. | (-3,0) | B. | (3,0) | C. | (2,0) | D. | (4,0) |
1.tan75°=( )
| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | 2-$\sqrt{3}$ |
18.设2a=3,2b=6,2c=12,则数列a,b,c是( )
| A. | 是等差数列,但不是等比数列 | B. | 是等比数列,但不是等差数列 | ||
| C. | 既是等差数列,又是等比数列 | D. | 非等差数列,又非等比数列 |
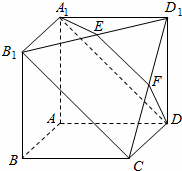 如图所示,在多面体A1B1D1-ABCD,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F
如图所示,在多面体A1B1D1-ABCD,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F