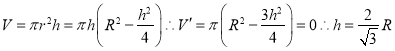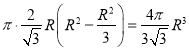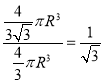题目内容
【题目】已知函数f（x）=ax3+cx（a＞0），其图象在点（1，f（1））处的切线与直线 x﹣6y+21=0垂直，导函数
f′（x）的最小值为﹣12．
（1）求函数f（x）的解析式；
（2）求y=f（x）在x∈[﹣2，2]的值域．
【答案】
（1）解：函数f（x）=ax3+cx的导数为f′（x）=3ax2+c，
其图象在点（1，f（1））处的切线斜率为k=3a+c，
切线与直线 x﹣6y+21=0垂直，可得3a+c=﹣6，
f′（x）的最小值为﹣12，即有c=﹣12，
解得，a=2，c=﹣12
（2）解：函数f（x）=2x3﹣12x的导数为f′（x）=6x2﹣12，
由f′（x）=0，可得x=± 
，
由f（ ）=﹣8 ，f（﹣ ）=8 ，
f（﹣2）=8，f（2）=﹣8．
可得f（x）在[﹣2，2]的最大值为8 ，最小值为﹣8 ．
即有函数的值域为[﹣8 ，8 ]
【解析】（1）求出函数的导数，求得切线的斜率，由两直线垂直的条件：斜率之积为﹣1，再由二次函数的最值求法，可得a，c的值；（2）求出导数，求得极值，以及端点处的函数值，即可得到值域．
练习册系列答案
相关题目
