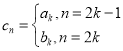题目内容
【题目】(本题满分16分)已知![]() ,
,![]() ,
,![]() 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足![]() ,
,![]() ,其中
,其中![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
(1)若数列![]() 是常数列,
是常数列,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() (
(![]() 是不为零的常数),求证:数列
是不为零的常数),求证:数列![]() 是等差数列;
是等差数列;
(3)若![]() (
(![]() 为常数,
为常数,![]() ),
),![]()
![]() ,求证:对任意的
,求证:对任意的![]() ,数列
,数列![]() 单调递减.
单调递减.
【答案】(1)![]() ;(2)详见解析;(3)详见解析;
;(2)详见解析;(3)详见解析;
【解析】
试题(1)由已知条件可化得数列![]() 的前
的前![]() 和,再作差求得通项,要注意分类讨论;(2)与(1)的思路相同,利用和作差,得到项之间的关系式,进而表示出数列
和,再作差求得通项,要注意分类讨论;(2)与(1)的思路相同,利用和作差,得到项之间的关系式,进而表示出数列![]() 的通项,利用等差数列的定义进行证明,还应注意补充说明
的通项,利用等差数列的定义进行证明,还应注意补充说明![]() ;(3)由(2)中和作差后的通项间的关系式可推得
;(3)由(2)中和作差后的通项间的关系式可推得![]() 与
与![]() 的关系式,则证得从第2项起
的关系式,则证得从第2项起![]() 成等比数列,求得其通项公式,同时也求得数列
成等比数列,求得其通项公式,同时也求得数列![]() 从第二项起是等差数列,所以从第2项起
从第二项起是等差数列,所以从第2项起![]() 为差比数列,通过作差或作商可以研究它的单调性;
为差比数列,通过作差或作商可以研究它的单调性;
试题解析:(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,
因为数列![]() 是各项不为零的常数列,所以
是各项不为零的常数列,所以![]() ,
,![]() ,
,
则由![]() 及
及![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,
,
当![]() 时,
时,![]() ,也满足
,也满足![]() ,故
,故![]() .
.
(2)因为![]() ,
,
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,
,
即![]() ,
,![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以当![]() 时,
时,![]() ,两式相减得
,两式相减得![]()
![]() ,
,
所以数列![]() 从第二项起是公差为
从第二项起是公差为![]() 等差数列;
等差数列;
又当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() 得
得![]() ,
,
故数列![]() 是公差为
是公差为![]() 等差数列.
等差数列.
(3)由(2)得当![]() 时,
时,![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,两式相减得
,两式相减得![]() ,
,
即![]() ,故从第二项起数列
,故从第二项起数列![]() 是等比数列,
是等比数列,
所以当![]() 时,
时,![]() ,
,
![]() ,
,
另外由已知条件得![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
所以![]() ,因而
,因而![]() ,令
,令![]()
![]() ,则
,则![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,所以对任意的
,所以对任意的![]() ,数列
,数列![]() 单调递减.
单调递减.

练习册系列答案
相关题目