Question

【题目】已知函数f(x)＝2cosxcos－sin2x＋sinxcosx.

(1)求f(x)的最小正周期；

(2)若关于x的方程在x∈上有两个不同的实根，求实数a的取值范围.

Answer 1

【答案】（1）；（2）．

【解析】试题分析：

（1）要求f(x)的最小正周期，需将f(x)＝2cosxcos(x－)－sin2x＋sinxcosx转化为y=A的形式.整理后得f(x)＝2sin，可知T＝π.

（2）主要考察函数零点问题，将转化为，作出在x∈的图像，即可知或.

试题解析：

(1)f(x)＝2cosxcos(x－)－sin2x＋sinxcosx＝cos2x＋sinxcosx－sin2x＋sinxcosx

＝cos2x＋sin2x＝2sin， ∴T＝π.

(2)

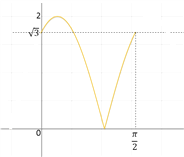
画出函数在x∈的图像，

由图可知或

故a的取值范围为.