题目内容
12．（x2+x+y）4的展开式中，x3y2的系数是12．（用数字作答）分析 在4个因式（x2+x+y）的乘积中，有2个因式选y，其余的2个因式中有一个选x，剩下的一个因式选x2，即可得到含x3y2的项，由此可得含x3y2的项系数．
解答 解：（x2+x+y）4 表示4个因式（x2+x+y）的乘积，在这4个因式中，有2个因式选y，其余的2个因式中有一个选x，剩下的一个因式选x2，
即可得到含x3y2的项，
故含x3y2的项系数是C24•C12•C11=12，
故答案为：12．
点评 本题主要考查二项式定理的应用，组合及组合数公式，属于基础题．
练习册系列答案
相关题目
2．在△ABC中，∠A=\frac{π}{3}，AB=2，且△ABC的面积为\frac{{\sqrt{3}}}{2}，则边AC的长为（ ）
| A． | 1 | B． | \sqrt{3} | C． | 2 | D． | 1 |
20．函数f（x）=\left\{\begin{array}{l}{{a}^{x}，（x＞1）}\\{（4-\frac{a}{2}）x+5，（x≤1）}\end{array}\right.满足对任意x1≠x2，都有\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}＞0成立，则实数a的取值范围是（ ）
| A． | （4，+∞） | B． | [6，8） | C． | （6，8） | D． | （1，8） |
4．
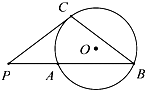如图，PC是⊙O的切线，C为切点，PAB为割线，PC=2，PA=1，∠P=60°，则BC=（ ）
如图，PC是⊙O的切线，C为切点，PAB为割线，PC=2，PA=1，∠P=60°，则BC=（ ）| A． | 3 | B． | 2 | C． | 3\sqrt{2} | D． | 2\sqrt{3} |