题目内容
已知函数f(x)=ax-ln x,g(x)= ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
(1)当a=1时,求函数f(x)的最小值;
(2)当a=1时,求证:f(m)>g(n)+ 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立;
(3)是否存在实数a,使得f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由.
 ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.(1)当a=1时,求函数f(x)的最小值;
(2)当a=1时,求证:f(m)>g(n)+
 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立;(3)是否存在实数a,使得f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由.
(1)1 (2)见解析 (3)见解析
解:(1)当a=1时,f(x)=x-ln x.
所以f′(x)=1-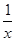 .
.
令f′(x)=0,得x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
所以当x=1时,f(x)min=1.
(2)证明:由(1)知,当m∈(0,e]时,
有f(m)≥1.
因为0<x≤e,所以g′(x)=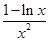 ≥0,
≥0,
即g(x)在区间(0,e]上为增函数,
所以g(x)≤g(e)=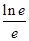 =
=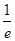 <
<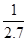 =
=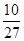 ,
,
所以g(x)+ <
<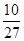 +
+ =1,
=1,
所以当m,n∈(0,e]时,
g(n)+ <1≤f(m).
<1≤f(m).
所以f(m)>g(n)+ 对一切m,n∈(0,e]恒成立.
对一切m,n∈(0,e]恒成立.
(3)假设存在实数a,使f(x)的最小值是3,则
f′(x)=a-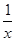 =
=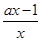 .
.
①当a≤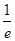 时,因为0<x≤e,所以ax≤1,
时,因为0<x≤e,所以ax≤1,
所以f′(x)≤0,所以f(x)在(0,e]上为减函数.
所以当x=e时,fmin(x)=ae-1=3,
解得a=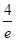 (舍去);
(舍去);
②当a>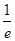 时,
时,
若0<x<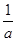 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在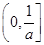 上为减函数;
上为减函数;
若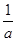 <x≤e时,f′(x)>0,f(x)在
<x≤e时,f′(x)>0,f(x)在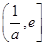 上为增函数.
上为增函数.
所以当x=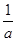 时,fmin(x)=1-ln
时,fmin(x)=1-ln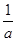 =3,解得a=e2.
=3,解得a=e2.
所以假设成立,存在实数a=e2,使得f(x)的最小值是3.
所以f′(x)=1-
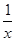 .
.令f′(x)=0,得x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (0,1) | 1 | (1,e] |
| f′(x) | - | 0 | + |
| f(x) | ? | 1 | ? |
所以当x=1时,f(x)min=1.
(2)证明:由(1)知,当m∈(0,e]时,
有f(m)≥1.
因为0<x≤e,所以g′(x)=
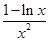 ≥0,
≥0,即g(x)在区间(0,e]上为增函数,
所以g(x)≤g(e)=
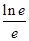 =
=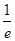 <
<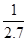 =
=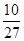 ,
,所以g(x)+
 <
<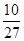 +
+ =1,
=1,所以当m,n∈(0,e]时,
g(n)+
 <1≤f(m).
<1≤f(m).所以f(m)>g(n)+
 对一切m,n∈(0,e]恒成立.
对一切m,n∈(0,e]恒成立.(3)假设存在实数a,使f(x)的最小值是3,则
f′(x)=a-
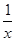 =
=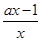 .
.①当a≤
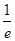 时,因为0<x≤e,所以ax≤1,
时,因为0<x≤e,所以ax≤1,所以f′(x)≤0,所以f(x)在(0,e]上为减函数.
所以当x=e时,fmin(x)=ae-1=3,
解得a=
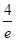 (舍去);
(舍去);②当a>
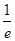 时,
时,若0<x<
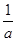 时,f′(x)<0,f(x)在
时,f′(x)<0,f(x)在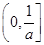 上为减函数;
上为减函数;若
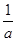 <x≤e时,f′(x)>0,f(x)在
<x≤e时,f′(x)>0,f(x)在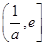 上为增函数.
上为增函数.所以当x=
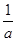 时,fmin(x)=1-ln
时,fmin(x)=1-ln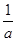 =3,解得a=e2.
=3,解得a=e2.所以假设成立,存在实数a=e2,使得f(x)的最小值是3.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
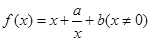 ,其中
,其中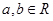 .
.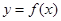 在点
在点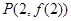 处的切线方程为
处的切线方程为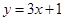 ,求函数
,求函数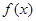 的解析式;
的解析式;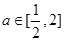 ,不等式
,不等式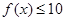 在
在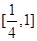 上恒成立,求
上恒成立,求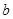 的取值范围.
的取值范围.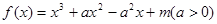
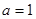 时,函数
时,函数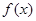 有三个互不相同的零点,求
有三个互不相同的零点,求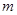 的取值范围;
的取值范围;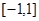 内没有极值点,求
内没有极值点,求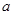 的取值范围;
的取值范围;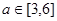 ,不等式
,不等式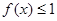 在
在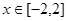 上恒成立,求实数
上恒成立,求实数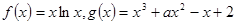
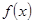 的单调区间;
的单调区间;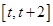
 上的最小值;
上的最小值;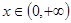 ,
,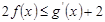 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. .
. 在点(1,f(1))处的切线方程;
在点(1,f(1))处的切线方程; ,且
,且 恒成立,求a的取值范围.
恒成立,求a的取值范围.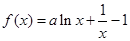 在
在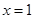 处取极值.
处取极值. 的值;
的值;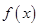 在
在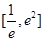 上的最大值和最小值.
上的最大值和最小值. 在R上存在导数
在R上存在导数 ,对任意的
,对任意的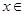 R,有
R,有 ,且
,且 )时,
)时, .若
.若 ,则实数a的取值范围为( )
,则实数a的取值范围为( ) ,g(x)=
,g(x)=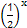 -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.