题目内容
已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
(1)求a,b,c,d的值;
(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
(1)a=4,b=2,c=2,d=2
(2)[1,e2]
(2)[1,e2]
(1)∵曲线y=f(x)和曲线y=g(x)都过点P(0,2),
∴b=d=2.
∵f′(x)=2x+a,故f′(0)=a=4.
∵g′(x)=ex(cx+d+c),
∴g′(0)=2+c=4,故c=2.
从而a=4,b=2,c=2,d=2.
(2)令F(x)=kg(x)-f(x),则F′(x)=(kex-1)(2x+4),
由题设可得F(0)≥0,故k≥1,
令F′(x)=0得x1=-ln k,x2=-2,
①若1≤k<e2,则-2<x1≤0,
从而当x∈[-2,x1)时,F′(x)<0,
当x∈(x1+∞)时,F′(x)>0,
即F(x)在[-2,+∞)上最小值为F(x1)=2x1+2-x22-4x1-2=-x1(x1+2)≥0,此时f(x)≤kg(x)恒成立;
②若k=e2,F′(x)=(ex+2-1)(2x+4),
故F(x)在[-2,+∞)上单调递增,
因为F(-2)=0,所以f(x)≤kg(x)恒成立;
③若k>e2,则F(-2)=-2ke-2+2=-2e-2(k-e2)<0,
从而当x∈[-2,+∞)时,
f(x)≤kg(x)不可能恒成立.
综上所述k的取值范围为[1,e2].
∴b=d=2.
∵f′(x)=2x+a,故f′(0)=a=4.
∵g′(x)=ex(cx+d+c),
∴g′(0)=2+c=4,故c=2.
从而a=4,b=2,c=2,d=2.
(2)令F(x)=kg(x)-f(x),则F′(x)=(kex-1)(2x+4),
由题设可得F(0)≥0,故k≥1,
令F′(x)=0得x1=-ln k,x2=-2,
①若1≤k<e2,则-2<x1≤0,
从而当x∈[-2,x1)时,F′(x)<0,
当x∈(x1+∞)时,F′(x)>0,
即F(x)在[-2,+∞)上最小值为F(x1)=2x1+2-x22-4x1-2=-x1(x1+2)≥0,此时f(x)≤kg(x)恒成立;
②若k=e2,F′(x)=(ex+2-1)(2x+4),
故F(x)在[-2,+∞)上单调递增,
因为F(-2)=0,所以f(x)≤kg(x)恒成立;
③若k>e2,则F(-2)=-2ke-2+2=-2e-2(k-e2)<0,
从而当x∈[-2,+∞)时,
f(x)≤kg(x)不可能恒成立.
综上所述k的取值范围为[1,e2].

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
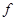 (
(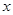 ) =
) =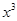 ,g (
,g (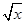 。
。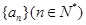 满足
满足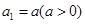 ,
,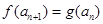 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的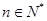 ,都有
,都有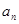 ≤
≤ 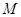 .
. 在R上存在导数
在R上存在导数 ,对任意的
,对任意的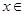 R,有
R,有 ,且
,且 )时,
)时, .若
.若 ,则实数a的取值范围为( )
,则实数a的取值范围为( ) ,g(x)=
,g(x)=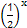 -m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.
-m.若?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是__________.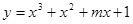 在实数集上是单调函数,则m的取值范围是 .
在实数集上是单调函数,则m的取值范围是 . ,其中
,其中 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;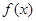 的单调区间及在
的单调区间及在 上的最大值.
上的最大值.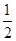 x2(a>0),若对任意两个不等的正实数x1,x2都有
x2(a>0),若对任意两个不等的正实数x1,x2都有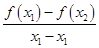 >2恒成立,则a的取值范围是________.
>2恒成立,则a的取值范围是________.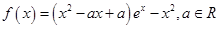 .
.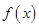 在
在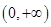 内单调递增,求
内单调递增,求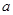 的取值范围;
的取值范围;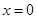 处取得极小值,求
处取得极小值,求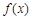 的导函数
的导函数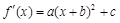 的图象如图所示,则函数
的图象如图所示,则函数