题目内容
在平面直角坐标系xoy中,已知椭圆C1: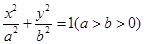 的左焦点为F1(-1,0),且点P(0,1)在C1上。
的左焦点为F1(-1,0),且点P(0,1)在C1上。
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2: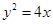 相切,求直线l的方程.
相切,求直线l的方程.
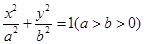 的左焦点为F1(-1,0),且点P(0,1)在C1上。
的左焦点为F1(-1,0),且点P(0,1)在C1上。(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:
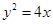 相切,求直线l的方程.
相切,求直线l的方程.(1) (2)l的方程为
(2)l的方程为 或
或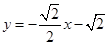
 (2)l的方程为
(2)l的方程为 或
或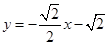
(1)由题意知: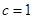 ,
,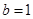 ,所以
,所以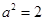 ,故椭圆C1的方程为
,故椭圆C1的方程为 .
.
(2)由题意知, 直线l的斜率必存在,设直线l的方程为 ,则
,则
由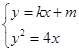 消
消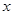 得:
得: ,因为直线l和抛物线C2:
,因为直线l和抛物线C2: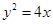 相切,
相切,
所以 且
且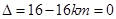 ,解得
,解得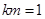
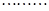 ①,
①,
由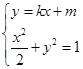 消
消 得:
得: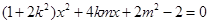 ,即
,即
 ,因为直线l与椭圆C1相切,所以
,因为直线l与椭圆C1相切,所以
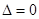 ,整理得:
,整理得: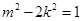
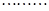 ②,解①②得:
②,解①②得: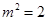 ,即
,即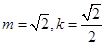 或
或
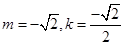 ,所以直线l的方程为
,所以直线l的方程为 或
或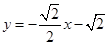 .
.
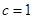 ,
,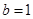 ,所以
,所以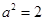 ,故椭圆C1的方程为
,故椭圆C1的方程为 .
.(2)由题意知, 直线l的斜率必存在,设直线l的方程为
 ,则
,则由
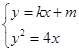 消
消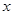 得:
得: ,因为直线l和抛物线C2:
,因为直线l和抛物线C2: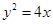 相切,
相切,所以
 且
且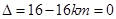 ,解得
,解得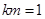
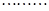 ①,
①,由
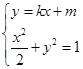 消
消 得:
得: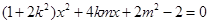 ,即
,即 ,因为直线l与椭圆C1相切,所以
,因为直线l与椭圆C1相切,所以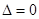 ,整理得:
,整理得: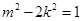
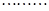 ②,解①②得:
②,解①②得: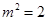 ,即
,即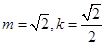 或
或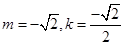 ,所以直线l的方程为
,所以直线l的方程为 或
或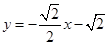 .
.
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 .如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
 的两个焦点,过F1的直线交椭圆于A、B两点,若
的两个焦点,过F1的直线交椭圆于A、B两点,若 ,则
,则 = _____________.
= _____________.  的离心率为
的离心率为 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为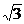 .
. 与椭圆C交于A、B两点,以
与椭圆C交于A、B两点,以 弦为直径的圆过坐标原点
弦为直径的圆过坐标原点 ,试探讨点
,试探讨点 的焦点为
的焦点为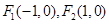 ,点
,点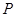 是椭圆
是椭圆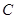 上的一点,
上的一点,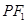 与
与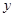 轴的交点
轴的交点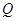 恰为
恰为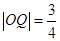 .
.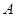 为椭圆的右顶点,过焦点
为椭圆的右顶点,过焦点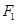 的直线与椭圆
的直线与椭圆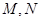 ,求
,求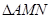 面积的取值范围.
面积的取值范围. 的左,右焦点,过F1的直线L与椭圆相交于A,B两点,|AB|=
的左,右焦点,过F1的直线L与椭圆相交于A,B两点,|AB|= ,直线L的斜率为1,则b的值为( )
,直线L的斜率为1,则b的值为( )



 的离心率为( )
的离心率为( )

 是椭圆
是椭圆 上的点,则
上的点,则 的取值范围是 .
的取值范围是 .