题目内容
(2011•山东)在平面直角坐标系xOy中,已知椭圆 .如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
(1)求m2+k2的最小值;
(2)若|OG|2=|OD|?|OE|,
(i)求证:直线l过定点;
(ii)试问点B,G能否关于x轴对称?若能,求出此时△ABG的外接圆方程;若不能,请说明理由.

 .如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).
.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点G,交直线x=﹣3于点D(﹣3,m).(1)求m2+k2的最小值;
(2)若|OG|2=|OD|?|OE|,
(i)求证:直线l过定点;
(ii)试问点B,G能否关于x轴对称?若能,求出此时△ABG的外接圆方程;若不能,请说明理由.

(1)2 (2)见解析
(1)设y=kx+t(k>0),
由题意,t>0,由方程组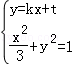 ,得(3k2+1)x2+6ktx+3t2﹣3=0,
,得(3k2+1)x2+6ktx+3t2﹣3=0,
由题意△>0,
所以3k2+1>t2,设A(x1,y1),B(x2,y2),
x1+x2=﹣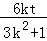 ,所以y1+y2=
,所以y1+y2=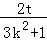 ,
,
∵线段AB的中点为E,∴xE=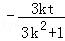 ,yE=
,yE=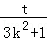 ,
,
此时kOE=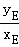 =﹣
=﹣ .
.
所以OE所在直线方程为y=﹣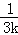 x,
x,
又由题设知D(﹣3,m).
令x=﹣3,得m= ,即mk=1,
,即mk=1,
所以m2+k2≥2mk=2,
(2)(i)证明:由(1)知OD所在直线方程为y=﹣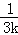 x,
x,
将其代入椭圆C的方程,并由k>0,解得G(﹣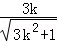 ,
,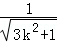 ),
),
又E( ,
, ),D(﹣3,
),D(﹣3, ),
),
由距离公式和t>0,得
|OG|2=(﹣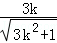 )2+(
)2+(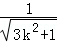 )2=
)2=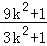 ,
,
|OD|=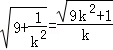 ,
,
|OE|=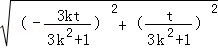 =
=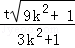 .
.
由|OG|2=|OD|?|OE|,
得t=k,
因此直线l的方程为y=k(x+1),
所以直线l恒过定点(﹣1,0);
(ii)由(i)得G(﹣ ,
,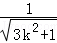 ),
),
若点B,G关于x轴对称,则B(﹣ ,﹣
,﹣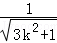 ),
),
将点B坐标代入y=k(x+1),
整理得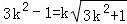 ,
,
即6k4﹣7k2+1=0,解得k2=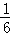 或k2=1,
或k2=1,
验证知k2=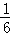 时,
时,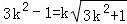 不成立,故舍去
不成立,故舍去
所以k2=1,又k>0,故k=1,
此时B(﹣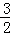 ,﹣
,﹣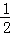 ),G(﹣
),G(﹣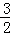 ,
,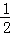 )关于x轴对称,
)关于x轴对称,
又由(I)得x1=0,y1=1,所以点A(0,1),
由于△ABG的外接圆的圆心在x轴上,可设△ABG的外接圆的圆心为(d,0),
因此d2+1=(d+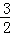 )2+
)2+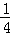 ,解得d=﹣
,解得d=﹣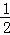 ,
,
故△ABG的外接圆的半径为r=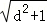 =
=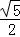 ,
,
所以△ABG的外接圆方程为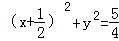 .
.
由题意,t>0,由方程组
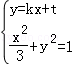 ,得(3k2+1)x2+6ktx+3t2﹣3=0,
,得(3k2+1)x2+6ktx+3t2﹣3=0,由题意△>0,
所以3k2+1>t2,设A(x1,y1),B(x2,y2),
x1+x2=﹣
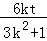 ,所以y1+y2=
,所以y1+y2=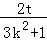 ,
,∵线段AB的中点为E,∴xE=
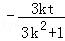 ,yE=
,yE=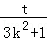 ,
,此时kOE=
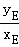 =﹣
=﹣ .
.所以OE所在直线方程为y=﹣
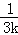 x,
x,又由题设知D(﹣3,m).
令x=﹣3,得m=
 ,即mk=1,
,即mk=1,所以m2+k2≥2mk=2,
(2)(i)证明:由(1)知OD所在直线方程为y=﹣
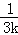 x,
x,将其代入椭圆C的方程,并由k>0,解得G(﹣
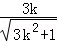 ,
,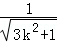 ),
),又E(
 ,
, ),D(﹣3,
),D(﹣3, ),
),由距离公式和t>0,得
|OG|2=(﹣
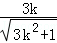 )2+(
)2+(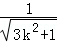 )2=
)2=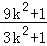 ,
,|OD|=
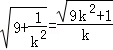 ,
,|OE|=
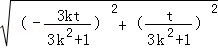 =
=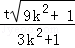 .
.由|OG|2=|OD|?|OE|,
得t=k,
因此直线l的方程为y=k(x+1),
所以直线l恒过定点(﹣1,0);
(ii)由(i)得G(﹣
 ,
,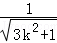 ),
),若点B,G关于x轴对称,则B(﹣
 ,﹣
,﹣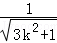 ),
),将点B坐标代入y=k(x+1),
整理得
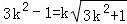 ,
,即6k4﹣7k2+1=0,解得k2=
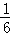 或k2=1,
或k2=1,验证知k2=
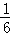 时,
时,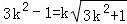 不成立,故舍去
不成立,故舍去所以k2=1,又k>0,故k=1,
此时B(﹣
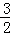 ,﹣
,﹣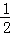 ),G(﹣
),G(﹣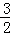 ,
,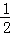 )关于x轴对称,
)关于x轴对称,又由(I)得x1=0,y1=1,所以点A(0,1),
由于△ABG的外接圆的圆心在x轴上,可设△ABG的外接圆的圆心为(d,0),
因此d2+1=(d+
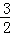 )2+
)2+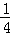 ,解得d=﹣
,解得d=﹣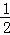 ,
,故△ABG的外接圆的半径为r=
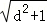 =
=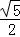 ,
,所以△ABG的外接圆方程为
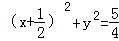 .
.
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 (
(  )的离心率为
)的离心率为 ,点(1,
,点(1, )在椭圆C上.
)在椭圆C上.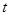 ),其中
),其中 ,切点分别是A、B,试利用结论:在椭圆
,切点分别是A、B,试利用结论:在椭圆 )处的椭圆切线方程是
)处的椭圆切线方程是 ,证明直线AB恒过椭圆的右焦点
,证明直线AB恒过椭圆的右焦点 ;
;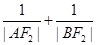 的值是否恒为常数,若是,求出此常数;若不是,请说明理由.
的值是否恒为常数,若是,求出此常数;若不是,请说明理由. 的左右焦点分别为
的左右焦点分别为 ,点
,点 为短轴的一个端点,
为短轴的一个端点, .
. 的方程;
的方程; ,且斜率为
,且斜率为 的直线
的直线 与椭圆
与椭圆 两点,
两点, 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线 于点
于点 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 .
. 为定值.
为定值.
 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 ;设
;设 为曲线
为曲线 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 两个不同的点.
两个不同的点. 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由; 的面积为
的面积为 ,
, 的面积为
的面积为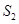 ,令
,令 ,求
,求 的最大值.
的最大值. 的右焦点重合,则该抛物线的准线方程为___________.
的右焦点重合,则该抛物线的准线方程为___________. 、
、 ,且
,且 是
是 与
与 的等差中项,则动点
的等差中项,则动点 的轨迹方程是( )
的轨迹方程是( )

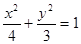

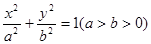 左右焦
左右焦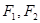 ,若椭圆C上恰有4个不同的点P,使得
,若椭圆C上恰有4个不同的点P,使得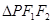 为等腰三角形,则C的离心率的取值范围是 _______
为等腰三角形,则C的离心率的取值范围是 _______  +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,则双曲线
,则双曲线 x
x  x
x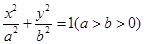 的左焦点为F1(-1,0),且点P(0,1)在C1上。
的左焦点为F1(-1,0),且点P(0,1)在C1上。 相切,求直线l的方程.
相切,求直线l的方程.