题目内容
已知椭圆 的一个焦点是
的一个焦点是 ,且截直线
,且截直线 所得弦长为
所得弦长为 ,求该椭圆的方程.
,求该椭圆的方程.
 的一个焦点是
的一个焦点是 ,且截直线
,且截直线 所得弦长为
所得弦长为 ,求该椭圆的方程.
,求该椭圆的方程.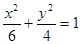
试题分析:由已知
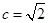 ,所以直线
,所以直线 过椭圆焦点,且垂直于
过椭圆焦点,且垂直于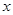 轴;
轴;由
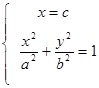 ,可得
,可得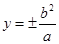 ,∴过焦点的弦长为
,∴过焦点的弦长为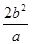 ,
,由
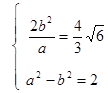 ,得
,得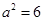 ,所以
,所以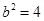 ,
,∴所求椭圆的方程为
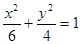 .
.点评:求出
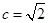 ,判断出直线
,判断出直线 过椭圆焦点,且垂直于
过椭圆焦点,且垂直于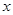 轴是解决此题的关键,还要注意椭圆中
轴是解决此题的关键,还要注意椭圆中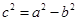 的应用.
的应用.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
题目内容
 的一个焦点是
的一个焦点是 ,且截直线
,且截直线 所得弦长为
所得弦长为 ,求该椭圆的方程.
,求该椭圆的方程.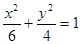
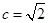 ,所以直线
,所以直线 过椭圆焦点,且垂直于
过椭圆焦点,且垂直于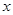 轴;
轴;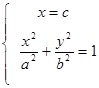 ,可得
,可得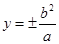 ,∴过焦点的弦长为
,∴过焦点的弦长为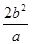 ,
,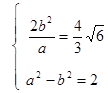 ,得
,得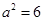 ,所以
,所以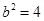 ,
,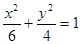 .
.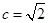 ,判断出直线
,判断出直线 过椭圆焦点,且垂直于
过椭圆焦点,且垂直于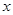 轴是解决此题的关键,还要注意椭圆中
轴是解决此题的关键,还要注意椭圆中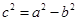 的应用.
的应用.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案