题目内容
【题目】已知函数f(x)=ln(x+ ![]() ),
),
(1)判断并证明函数y=f(x)的奇偶性;
(2)判断并证明函数y=f(x)在R上的单调性;
(3)当x∈[1,2]时,不等式f(a4x)+f(2x+1)>0恒成立,求实数a的取值范围.
【答案】
(1)解:函数f(x)=ln(x+ ![]() )为奇函数.
)为奇函数.
要使函数有意义,则 ![]() ,
,
∵ ![]() ,
,
∴ ![]() 的解集为R,即函数f(x)的定义域为R,
的解集为R,即函数f(x)的定义域为R,
又 ![]() ,
,
∴函数y=f(x)是奇函数
(2)解:设x1,x2∈[0,+∞),且x1<x2,
则 ![]() ,
,
∵0≤x1<x2,
∴ ![]() ,
,
∴ ![]() ,
,
即 ![]() ,
,
∴f(x1)<f(x2).
∴函数y=f(x)在[0,+∞)上为增函数,
又f(x)为奇函数,
∴函数y=f(x)在R上为增函数
(3)解:不等式f(a4x)+f(2x+1)>0等价于f(a4x)>﹣f(2x+1).
∵f(﹣x)=﹣f(x),
∴f(a4x)>f(﹣2x﹣1).
函数y=f(x)在R上为增函数,
∴原不等式等价于a4x>﹣2x﹣1,
即 ![]() 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
只需 ![]() .
.
令 ![]() ,
,
由复合函数的单调性知, ![]() 在区间[1,2]上为增函数.
在区间[1,2]上为增函数.
∴当x=2时, ![]() .
.
即 ![]() .
.
【解析】(1)求出函数的定义域,然后结合f(﹣x)=﹣f(x)可得函数的奇偶性;(2)直接利用函数单调性的定义证明;(3)把不等式f(a4x)+f(2x+1)>0转化为f(a4x)>﹣f(2x+1),结合函数是奇函数得到 ![]() ,由复合函数的单调性求得
,由复合函数的单调性求得 ![]() 在区间[1,2]上的最大值,则答案可求.
在区间[1,2]上的最大值,则答案可求.
【考点精析】通过灵活运用函数单调性的判断方法和函数奇偶性的性质,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体![]() 名学生中随机抽取了
名学生中随机抽取了![]() 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.
年级名次 是否近视 |
|
|
近视 |
|
|
不近视 |
|
|
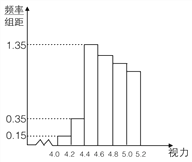
(1)若直方图中后四组的频数成等差数列,试估计全 年级视力在![]() 以下的人数;
以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在![]() 名和
名和![]() 名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过
名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过![]() 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系?
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
附: 
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
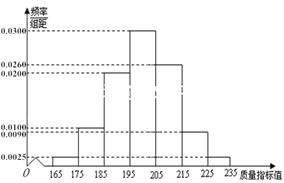
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体![]() 名学生中随机抽取了
名学生中随机抽取了![]() 名学生的体检表,并得到如图的频率分布直方图.
名学生的体检表,并得到如图的频率分布直方图.
年级名次 是否近视 |
|
|
近视 |
|
|
不近视 |
|
|
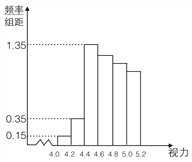
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在![]() 以下的人数;
以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在![]() 名和
名和![]() 名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过
名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过![]() 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系?
(3)在(Ⅱ)中调查的![]() 名学生中,按照分层抽样在不近视的学生中抽取了
名学生中,按照分层抽样在不近视的学生中抽取了![]() 人,进一步调查他们良好的护眼习惯,并且在这
人,进一步调查他们良好的护眼习惯,并且在这![]() 人中任取
人中任取![]() 人,记名次在
人,记名次在![]() 的学生人数为
的学生人数为![]() ,求
,求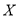 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
| 7.879 |
![]()
附: