题目内容
函数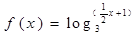 的单调递增区间为_______________.
的单调递增区间为_______________.
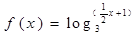 的单调递增区间为_______________.
的单调递增区间为_______________.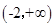
试题分析:根据题意,由于函数
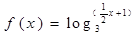 ,外层是底数为3的对数函数,单调递增,内层是一次函数,递增,那么则可知函数的增区间就是函数的定义域,因为
,外层是底数为3的对数函数,单调递增,内层是一次函数,递增,那么则可知函数的增区间就是函数的定义域,因为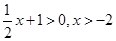 ,故可知函数
,故可知函数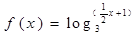 的单调递增区间为
的单调递增区间为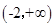 。
。点评:解决该试题的关键是对于复合函数单调性的判定:同增异减。

练习册系列答案
相关题目
题目内容
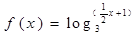 的单调递增区间为_______________.
的单调递增区间为_______________.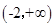
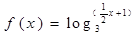 ,外层是底数为3的对数函数,单调递增,内层是一次函数,递增,那么则可知函数的增区间就是函数的定义域,因为
,外层是底数为3的对数函数,单调递增,内层是一次函数,递增,那么则可知函数的增区间就是函数的定义域,因为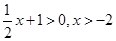 ,故可知函数
,故可知函数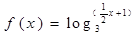 的单调递增区间为
的单调递增区间为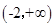 。
。