题目内容
已知函数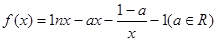 .
.
(Ⅰ)当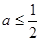 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅱ)设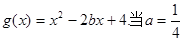 时,若对任意
时,若对任意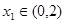 ,存在
,存在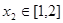 ,使
,使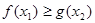 ,求实数
,求实数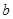 的取值范围.
的取值范围.
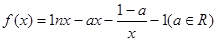 .
.(Ⅰ)当
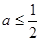 时,讨论
时,讨论 的单调性;
的单调性;(Ⅱ)设
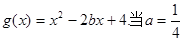 时,若对任意
时,若对任意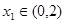 ,存在
,存在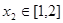 ,使
,使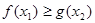 ,求实数
,求实数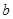 的取值范围.
的取值范围.(Ⅰ)当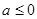 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;
当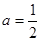 时,函数
时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;
当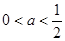 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在
在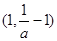 上单调递增;
上单调递增;
函数 上单调递减,
上单调递减,
(Ⅱ)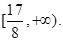
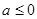 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;函数
 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;当
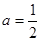 时,函数
时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;当
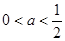 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减; 函数
 在
在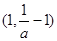 上单调递增;
上单调递增;函数
 上单调递减,
上单调递减,(Ⅱ)
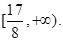
试题分析:(Ⅰ)因为
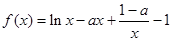
所以
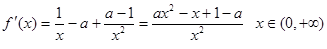
令
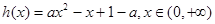
(1)当
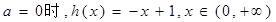
所以,当
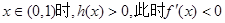 ,函数
,函数 单调递减;
单调递减;当
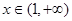 时,
时,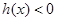 ,此时
,此时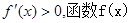 单调递
单调递(2)当
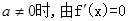
即
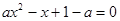 ,解得
,解得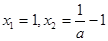
①当
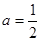 时,
时, 恒成立,
恒成立,此时
 ,函数
,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;②当
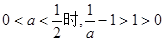
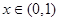 时,
时,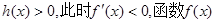 单调递减;
单调递减;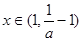 时,
时,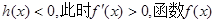 单调递增;
单调递增;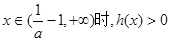 ,此时
,此时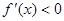 ,函数
,函数 单调递减;
单调递减;③当
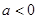 时,由于
时,由于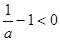
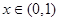 时,
时,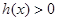 ,此时
,此时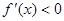 ,函数
,函数 单调递减;
单调递减;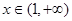 时,
时,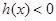 ,此时
,此时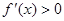 ,函数
,函数 单调递增。
单调递增。综上所述:
当
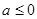 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;函数
 在(1,+∞)上单调递增;
在(1,+∞)上单调递增;当
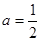 时,函数
时,函数 在(0,+∞)上单调递减;
在(0,+∞)上单调递减;当
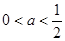 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减; 函数
 在
在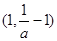 上单调递增;
上单调递增;函数
 上单调递减,
上单调递减,(Ⅱ)因为
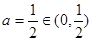 ,由(Ⅰ)知,
,由(Ⅰ)知,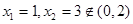 ,当
,当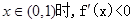 ,
,函数
 单调递减;当
单调递减;当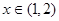 时,
时,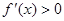
函数
 单调递增,所以
单调递增,所以 在(0,2)上的最小值为
在(0,2)上的最小值为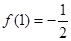
由于“对任意
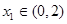 ,存在
,存在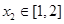 ,使
,使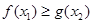 ”等价于
”等价于“
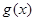 在[1,2]上的最小值不大于
在[1,2]上的最小值不大于 在(0,2)上的最小值
在(0,2)上的最小值 ” (*)
” (*)又
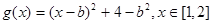 ,所以
,所以①当
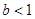 时,因为
时,因为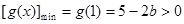 ,此时与(*)矛盾;
,此时与(*)矛盾;②当
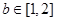 时,因为
时,因为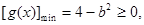 ,同样与(*)矛盾;
,同样与(*)矛盾;③当
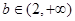 时,因为
时,因为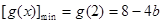
解不等式
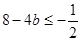 ,可得
,可得
综上,
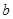 的取值范围是
的取值范围是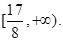
点评:典型题,本题属于导数应用中的基本问题,恒成立问题,往往通过“分离参数”,转化成求函数的最值。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
相关题目
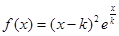 .
.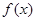 的单调区间;
的单调区间;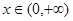 ,有
,有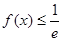 恒成立,求
恒成立,求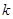 的取值范围.
的取值范围.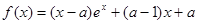 ,
,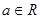 。
。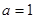 时,求
时,求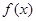 的单调区间;
的单调区间;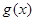 是
是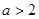 时,在
时,在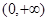 上恰有一个
上恰有一个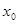 使得
使得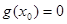 ;
;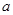 的取值范围,使得对任意的
的取值范围,使得对任意的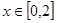 ,恒有
,恒有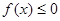 成立。
成立。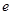 为自然对数的底数。
为自然对数的底数。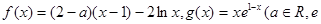 为自然对数的底数).
为自然对数的底数).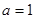 时,求
时,求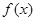 的单调区间;若函数
的单调区间;若函数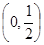 上无零点,求
上无零点,求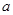 最小值;
最小值;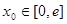 ,在
,在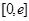 上总存在两个不同的
上总存在两个不同的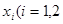 ),使
),使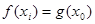 成立,求
成立,求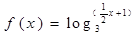 的单调递增区间为_______________.
的单调递增区间为_______________.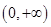 上为减函数的是( )
上为减函数的是( )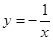
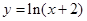
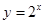
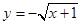
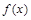 对任意
对任意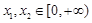
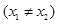 ,有
,有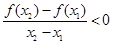 ,则
,则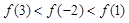
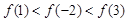
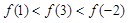
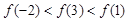
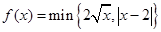 ,其中
,其中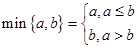 ,若动直线
,若动直线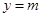 与函数
与函数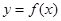 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为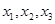 ,则
,则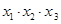 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.