Question

14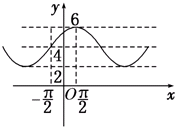．已知函数f（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（　　）

• A． y=2cos（$\frac{x}{2}$-$\frac{π}{4}$）+4
• B． y=2cos（$\frac{x}{2}$+$\frac{π}{4}$）+4
• C． y=4cos（$\frac{x}{2}$-$\frac{π}{4}$）+2
• D． y=4cos（$\frac{x}{2}$+$\frac{π}{4}$）+2

Answer 1

分析 先根据函数的最大值和最小值求得A和B，然后利用图象中$\frac{π}{2}$-（-$\frac{π}{2}$）求得函数的周期，求得ω，最后根据x=$\frac{π}{2}$时取最大值，求得φ，即可得解．

解答 解：如图根据函数的最大值和最小值得|A|+B=6，|A|-B=-2，、
∵A＞0，
∴A=2，B=4，
函数的周期为[$\frac{π}{2}$-（-$\frac{π}{2}$）]×4=4π，
又∵ω＞0，
∴ω=$\frac{1}{2}$，
当x=$\frac{π}{2}$时取最大值，即cos（2×$\frac{π}{2}$+φ）=1，2×$\frac{π}{2}$+φ=2kπ，k∈Z，
∴φ=2kπ-$\frac{π}{4}$，k∈Z，
∵|φ|＜$\frac{π}{2}$，
∴φ=-$\frac{π}{4}$，
∴解析式为：y=2cos（$\frac{1}{2}$x-$\frac{π}{4}$）+4．
故选：A．

点评 本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，考查了学生基础知识的运用和图象观察能力，属于基本知识的考查．