题目内容
9.已知圆C:x2+y2-2x+my=0,其圆心C在直线y=x上.(Ⅰ)求m的值;
(Ⅱ)若过点(-1,1)的直线l与圆C相切,求直线l的方程.
分析 (Ⅰ)求出圆的标准方程,求出圆心坐标,代入直线方程,即可求m的值;
(Ⅱ)p判断直线l的斜率存在,设出直线l的方程.利用直线l和圆C相切,求出k,即可求直线l的方程.
解答 (本小题满分12分)
解:(Ⅰ)圆C的标准方程为:${(x-1)^2}+{(y+\frac{m}{2})^2}=1+\frac{m^2}{4}$,
所以,圆心为$(1,-\frac{m}{2})$
由圆心C在直线y=x上,得 m=-2.…(5分)
所以,圆C的方程为:(x-1)2+(y-1)2=2.
(Ⅱ)由题意可知直线l的斜率存在,设直线l的方程为:y-1=k(x+1),即kx-y+k+1=0,
由于直线l和圆C相切,得$\sqrt{2}=\frac{{|{2k}|}}{{\sqrt{{k^2}+1}}}$…(8分)
解得:k=±1
所以,直线方程为:x-y+2=0或x+y=0.…(12分)
点评 本题考查直线与圆的方程的综合应用,圆的切线方程的求法,考查计算能力.

练习册系列答案
相关题目
14.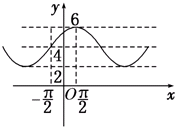 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | y=2cos($\frac{x}{2}$-$\frac{π}{4}$)+4 | B. | y=2cos($\frac{x}{2}$+$\frac{π}{4}$)+4 | C. | y=4cos($\frac{x}{2}$-$\frac{π}{4}$)+2 | D. | y=4cos($\frac{x}{2}$+$\frac{π}{4}$)+2 |
1.给出的下列函数中在$(\frac{π}{2},π)$上是增函数的是( )
| A. | y=sinx | B. | y=cosx | C. | y=sin2x | D. | y=cos2x |