题目内容
3．已知Sn是等差数列{an}的前n项和，S3=6，an-2+an=16，若Sn=50，则n的值为10．分析 通过S3=3a2=6可得a2=2，利用an-2+an=16可得公差d=$\frac{6}{n-3}$，利用Sn=50计算即得结论．
解答 解：∵S3=3a2=6，∴a2=2，
又an-2+an=16，
化为：a2+d（n-4）+a2+d（n-2）=16，
∴4+d（2n-6）=16，
即d（n-3）=6，
∴d=$\frac{6}{n-3}$，
而Sn=na1+$\frac{n（n-1）}{2}$d=n（2-$\frac{6}{n-3}$）+$\frac{3n（n-1）}{n-3}$=50，
化简得：（n-3）（n-10）=0，
解得n=10或n=3（增根，舍去），
故答案为：10．
点评 本题考查等差数列的相关知识，注意解题方法的积累，属于中档题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13．已知f1（x）=sinx，f2（x）=f1′（x），f3（x）=f2′（x），f4（x）=f3′（x），…，fn（x）=fn-1′（x），则f2015（x）等于（ ）
| A． | cosx | B． | -cosx | C． | sinx | D． | -sinx |
14．
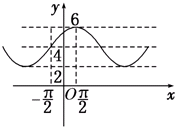已知函数f（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）
已知函数f（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）| A． | y=2cos（$\frac{x}{2}$-$\frac{π}{4}$）+4 | B． | y=2cos（$\frac{x}{2}$+$\frac{π}{4}$）+4 | C． | y=4cos（$\frac{x}{2}$-$\frac{π}{4}$）+2 | D． | y=4cos（$\frac{x}{2}$+$\frac{π}{4}$）+2 |
12．在△ABC中，已知M是BC中点，设$\overrightarrow{CB}$=$\overrightarrow{a}$，$\overrightarrow{CA}$=$\overrightarrow{b}$，则$\overrightarrow{AM}$=（ ）
| A． | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | B． | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | C． | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D． | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |