题目内容
6．定义两种运算：a⊕b=$\sqrt{{a^2}-{b^2}}$，a?b=$\sqrt{{{（a-b）}^2}}$，则函数f（x）=$\frac{2⊕x}{（x?2）-2}$的图象关于原点 对称．分析 根据定义先求出f（x）的表达式，然后判断函数的奇偶性即可．
解答 解：由定义得f（x）=$\frac{2⊕x}{（x?2）-2}$=$\frac{\sqrt{4-{x}^{2}}}{\sqrt{（x-2）^{2}-2}}=\frac{\sqrt{4-{x}^{2}}}{|x-2|-2}$，
由4-x2≥0得-2≤x≤2，
则f（x）=$\frac{\sqrt{2-{x}^{2}}}{2-x-2}$=$-\frac{\sqrt{4-{x}^{2}}}{x}$，
又x≠0，则函数的定义域为[-2，0）∪（0，2]，定义域关于原点对称，
则f（-x）=-$\frac{\sqrt{4-（-x）^{2}}}{-x}$=$\frac{\sqrt{4-{x}^{2}}}{x}$=-f（x），
即f（-x）=-f（x），则函数f（x）是奇函数，
故f（x）的图象关于原点对称，
故答案为：原点
点评 本题主要考查函数奇偶性的判断，根据定义运算，求出函数的解析式是解决本题的关键．
练习册系列答案
相关题目
14．
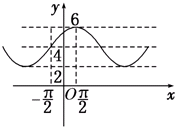已知函数f（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）
已知函数f（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为（ ）| A． | y=2cos（$\frac{x}{2}$-$\frac{π}{4}$）+4 | B． | y=2cos（$\frac{x}{2}$+$\frac{π}{4}$）+4 | C． | y=4cos（$\frac{x}{2}$-$\frac{π}{4}$）+2 | D． | y=4cos（$\frac{x}{2}$+$\frac{π}{4}$）+2 |
1．给出的下列函数中在$（\frac{π}{2}，π）$上是增函数的是（ ）
| A． | y=sinx | B． | y=cosx | C． | y=sin2x | D． | y=cos2x |