题目内容
19.已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.(Ⅰ)求a、b的值;
(Ⅱ)求函数f(x)在区间[-2,2]上的最大值和最小值.
分析 (Ⅰ)f'(x)=3ax2+2bx-3,依题意,f'(1)=f'(-1)=0,解出即可.
(Ⅱ)f(x)=x3-3x,f'(x)=3x2-3=3(x+1)(x-1).利用导数研究其在区间[-2,2]的单调性极值与最值即可得出.
解答 解:(Ⅰ)f'(x)=3ax2+2bx-3,
依题意,f'(1)=f'(-1)=0,即$\left\{\begin{array}{l}{3a+2b-3=0}\\{3a-2b-3=0}\end{array}\right.$,
解得a=1,b=0.
(Ⅱ)f(x)=x3-3x,f'(x)=3x2-3=3(x+1)(x-1).
令f'(x)=0,得x=-1,x=1.
若x∈[-2,-1)∪(1,2],则f'(x)>0,故f(x)在[-2,-1),(1,2)上是增函数,
若x∈(-1,1),则f'(x)<0,故f(x)在(-1,1)上是减函数.
∴f(-1)=2是极大值;f(1)=-2是极小值;
又f(2)=2,f(-2)=-2.
∴最大值为2,最小值为-2.
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
14.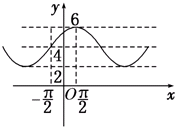 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | y=2cos($\frac{x}{2}$-$\frac{π}{4}$)+4 | B. | y=2cos($\frac{x}{2}$+$\frac{π}{4}$)+4 | C. | y=4cos($\frac{x}{2}$-$\frac{π}{4}$)+2 | D. | y=4cos($\frac{x}{2}$+$\frac{π}{4}$)+2 |
9.已知sinα=-$\frac{1}{3}$,且α∈(-$\frac{π}{2}$,$\frac{π}{2}}$),则tanα=( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $-\frac{{\sqrt{2}}}{4}$ | C. | $±\frac{{\sqrt{2}}}{4}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
 如图所示的流程图是将一系列指令和问题用框图的形式排列而成的.阅读下面的流程图,并回答下列问题.若b>c>a,则输出的数是b.
如图所示的流程图是将一系列指令和问题用框图的形式排列而成的.阅读下面的流程图,并回答下列问题.若b>c>a,则输出的数是b.