题目内容
2.已知0<x<π,sinα、cosα是方程5x2-x+m=0的两实根,求:(1)m的值;
(2)求sinα、cosα、tanα的值;
(3)sin3α+cos3α的值.
分析 (1)根据题意,利用韦达定理及同角三角函数间基本关系列出关系式,整理即可求出m的值;
(2)利用完全平方公式及同角三角函数间基本关系列出关系式,整理求出sinα-cosα的值,与已知等式联立求出sinα与cosα的值,即可确定出tanα的值;
(3)原式利用立方和公式变形,再利用同角三角函数间基本关系化简,将各自的值代入计算即可求值.
解答 解:(1)∵0<α<π,sinα、cosα是方程5x2-x+m=0的两实根,
∴sinα+cosα=$\frac{1}{5}$,sinαcosα=$\frac{m}{5}$,
∵(sinα+cosα)2=1+2sinαcosα=1+$\frac{2m}{5}$=$\frac{1}{25}$,
解得:m=-$\frac{12}{5}$;
(2)∵sinα+cosα=$\frac{1}{5}$①,sinαcosα=-$\frac{12}{25}$,
∴(sinα-cosα)2=1-2sinαcosα=1+$\frac{24}{25}$=$\frac{49}{25}$,
∴sinα-cosα=$\frac{7}{5}$②,
联立①②解得:sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,tanα=-$\frac{4}{3}$;
(3)∵sinα+cosα=$\frac{1}{5}$,sinαcosα=-$\frac{12}{25}$,
∴原式=(sinα+cosα)(sin2α-sinαcosα+cos2α)=(sinα+cosα)(1-sinαcosα)=$\frac{1}{5}$×$\frac{37}{25}$=$\frac{37}{125}$.
点评 此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 正三角形 |
| A. | cosx | B. | -cosx | C. | sinx | D. | -sinx |
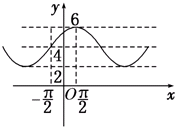 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | y=2cos($\frac{x}{2}$-$\frac{π}{4}$)+4 | B. | y=2cos($\frac{x}{2}$+$\frac{π}{4}$)+4 | C. | y=4cos($\frac{x}{2}$-$\frac{π}{4}$)+2 | D. | y=4cos($\frac{x}{2}$+$\frac{π}{4}$)+2 |
| A. | $\frac{1}{2}$$\overrightarrow{a}$-$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | C. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |