题目内容
已知抛物线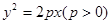 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
A. +1 +1 | B. +l +l |
C. | D. |
A
解析试题分析:由抛物线的定义可得A到抛物线的焦点F的距离为p,故AF垂直于x轴,把x= 代入y2=2px解得点A的坐标,再由椭圆的定义求得椭圆的离心率e=
代入y2=2px解得点A的坐标,再由椭圆的定义求得椭圆的离心率e= 的值解:由题可得图,设椭圆另一焦点为E,因为抛物线y2=2px(p>0)的焦点F(
的值解:由题可得图,设椭圆另一焦点为E,因为抛物线y2=2px(p>0)的焦点F( ,0).由抛物线的定义可得A到抛物线的焦点F的距离为p,故AF垂直于x轴.把x=
,0).由抛物线的定义可得A到抛物线的焦点F的距离为p,故AF垂直于x轴.把x= 代入y2=2px解得y=±p,所以A(
代入y2=2px解得y=±p,所以A( ,p),同时点F(-
,p),同时点F(- ,0),那么可知|AF|=p,由双曲线的定义可知AE=
,0),那么可知|AF|=p,由双曲线的定义可知AE= P,那么可知e=
P,那么可知e= +1,选A.
+1,选A.
考点:抛物线、双曲线的定义
点评:本题主要考查抛物线、双曲线的定义、标准方程,以及它们的简单性质的应用,在做圆锥曲线问题时,用定义来解题是比较常用的方法,属于中档题

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知双曲线 ,其右焦点为
,其右焦点为 ,
, 为其上一点,点
为其上一点,点 满足
满足 =1,
=1,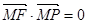 ,则
,则 的最小值为 ( )
的最小值为 ( )
| A.3 | B. | C.2 | D. |
焦点在x轴上的椭圆 的离心率的最大值为( )
的离心率的最大值为( )
A. | B. | C.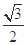 | D. |
已知点P是双曲线C: 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
A.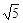 | B.2 | C. | D.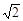 |
双曲线 ( )
( )
A. | B. | C. | D. |
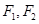 分别是双曲线
分别是双曲线 的两个焦点,
的两个焦点, 和
和 是以
是以 (
( 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且 是等边三角形,则双曲线的离心率为( )
是等边三角形,则双曲线的离心率为( )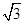



 交于A,B两点,若△FAB为直角三角形,则双曲线的离心率是
交于A,B两点,若△FAB为直角三角形,则双曲线的离心率是


 的左焦点
的左焦点 ,作圆:
,作圆: 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) 



 的右支上一点,M、N分别是圆(x+5)2+y2=4和
的右支上一点,M、N分别是圆(x+5)2+y2=4和