题目内容
过双曲线 的左焦点
的左焦点 ,作圆:
,作圆: 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. | B. | C. | D. |
A
解析试题分析:∵ ,
,
∴E为PF的中点,令右焦点为F′,则O为FF′的中点,
则|PF′|=2|OE|=a,
∵E为切点,∴OE⊥PF,∴PF′⊥PF。
∵|PF|-|PF′|=2a
∴|PF|=|PF′|+2a=3a
在Rt△PFF′中,|PF|2+|PF′|2=|FF′|2,即9a2+a2=4c2,
所以离心率e= ,故选A。.
,故选A。.
考点:双曲线的定及其几何性质、圆的方程等基础知识。
点评:中档题,注意运用数形结合思想、化归与转化思想,在圆锥曲线中,求离心率关键就是求参数a,b,c的关系.

练习册系列答案
相关题目
双曲线 过其左焦点F1作x轴的垂线交双曲线于A,B两点,若双曲线右顶点在以AB为直径的圆内,则双曲线离心率的取值范围为
过其左焦点F1作x轴的垂线交双曲线于A,B两点,若双曲线右顶点在以AB为直径的圆内,则双曲线离心率的取值范围为
| A.(2,+∞) | B.(1,2) |
C.( ,+∞) ,+∞) | D.(1, ) ) |
若抛物线 上一点到焦点和抛物线对称轴的距离分别为
上一点到焦点和抛物线对称轴的距离分别为 和
和 ,则抛物线方程为( )
,则抛物线方程为( )
A. | B. |
C. 或 或 | D. 或 或 |
已知抛物线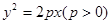 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
有相同的焦点F,点A是两曲线的交点,且|AF|=p,则双曲线的离心率为( )
A. +1 +1 | B. +l +l |
C. | D. |
角 的终边经过点A
的终边经过点A ,且点A在抛物线
,且点A在抛物线 的准线上,则
的准线上,则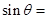 ( )
( )
A. | B. | C. | D. |
已知实数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B.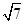 | C. 或 或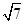 | D. 或7 或7 |
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,若椭圆
,若椭圆 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆



 的离心率为
的离心率为 . 双曲线
. 双曲线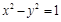 的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )



 分别为双曲线
分别为双曲线 的左右焦点,点P在双曲线的右支上,且
的左右焦点,点P在双曲线的右支上,且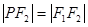 ,
, 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( )


