题目内容
【题目】已知函数![]() ,其导函数设为
,其导函数设为![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,若![]() 的极值点恰为
的极值点恰为![]() 的零点,试求
的零点,试求![]() ,
,![]() 这两个函数的所有极值之和的取值范围.
这两个函数的所有极值之和的取值范围.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)根据题意,求出导数,解关于导数的不等式,即可求函数![]() 的单调区间。
的单调区间。
(Ⅱ)根据![]() 有两个极值点
有两个极值点![]() ,
,![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,利用韦达定理以及极值点对应的导函数的值为0,得
,利用韦达定理以及极值点对应的导函数的值为0,得![]() ,
,![]() ,将
,将![]() 表达成
表达成![]() ,再代入各项对应得值即可。
,再代入各项对应得值即可。
(Ⅲ)根据题意,解出![]() 的极值点,代入
的极值点,代入![]() ,可得
,可得![]() 与
与![]() 的等量关系,再结合(Ⅱ)中的不等关系解出
的等量关系,再结合(Ⅱ)中的不等关系解出![]() 的范围,将
的范围,将![]() ,
,![]() 这两个函数的所有极值之和用
这两个函数的所有极值之和用![]() 表达出来,构造一个新的关于
表达出来,构造一个新的关于![]() 的函数,利用导数,即可求
的函数,利用导数,即可求![]() ,
,![]() 这两个函数的所有极值之和的取值范围。
这两个函数的所有极值之和的取值范围。
(Ⅰ)![]() ,
,![]() .
.
若![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,方程
,方程![]() 有两个不等实根
有两个不等实根![]() ,
,![]()
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增 ;
上单调递增 ;
(Ⅱ)因![]() 有两个极值点
有两个极值点![]() ,
,![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,
,
且![]() ,
,![]() ,
,![]() .
.
于是,![]()
![]() .
.
(Ⅲ)由![]() ,则
,则![]() 的极值点为
的极值点为![]() .
.
于是,![]() ,即
,即![]() .显然,
.显然,![]() ,则
,则![]() .
.
由(Ⅱ)知,![]() ,
,![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() .
.
于是,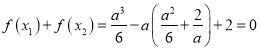 .
.
故![]() ,
,![]() 的所有极值之和为
的所有极值之和为![]() ,
,
因![]() ,若
,若![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
故![]() .
.
若![]() ,知
,知![]() 时有
时有![]() ,则
,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() .
.
因此,当![]() 时,所求的取值范围为
时,所求的取值范围为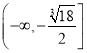 .当
.当![]() 时,所求的取值范围为
时,所求的取值范围为![]() ,
,
综上,![]() ,
,![]() 这两个函数的所有极值之和的取值范围是
这两个函数的所有极值之和的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】随机调查某社区80个人,以研究这一社区居民在晚上8点至十点时间段的休闲方式与性别的关系,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,求这3人中至少有1人是以看书为休闲方式的概率;
(2)根据以上数据,能否有99%的把握认为“在晚上8点至十点时间段的休闲方式与性别有关系?”
参考公式: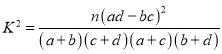 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |