题目内容
【题目】在三棱锥P﹣ABC中,D为AB的中点.
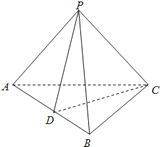
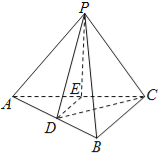
(1)与BC平行的平面PDE交AC于点E,判断点E在AC上的位置并说明理由如下:
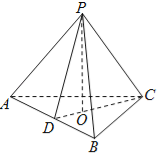
(2)若PA=PB,且△PCD为锐角三角形,又平面PCD⊥平面ABC,求证:AB⊥PC.
【答案】(1)![]() 为
为![]() 中点(2)详见解析
中点(2)详见解析
【解析】试题分析:(1)根据线面平行的性质进行判断即可:
(2)根据面面垂直的性质定理进行证明.
(1)解:E为AC中点.理由如下:
平面PDE交AC于E,
即平面PDE∩平面ABC=DE,
而BC∥平面PDF,BC平面ABC,
所以BC∥DE,
在△ABC中,因为D为AB的中点,所以E为AC中点;
(2)证:因为PA=PB,D为AB的中点,
所以AB⊥PD,
因为平面PCD⊥平面ABC,平面PCD∩平面ABC=CD,
在锐角△PCD所在平面内作PO⊥CD于O,
则PO⊥平面ABC,
因为AB平面ABC,
所以PO⊥AB
又PO∩PD=P,PO,PD平面PCD,
则AB⊥平面PCD,
又PC平面PCD,
所以AB⊥PC.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目