题目内容
3.给出下列四个命题中:①命题:$?x∈R,sinx-cosx=\sqrt{2}$;
②函数f(x)=2x-x2有三个零点;
③对?(x,y)∈{(x,y)|4x+3y-10=0},则x2+y2≥4.
④已知函数$f(x)=x+\frac{1}{x}$,若△ABC中,角C是钝角,那么f(sinA)>f(cosB)
其中所有真命题的序号是①②③④.
分析 求出sinx-cosx的值域,可判断①; 画出y=2x,y=x2的图象,数形结合,可判断②;求出圆心到直线的距离,可判断③;利用函数的单调性,判断两个函数值的大小,可判断④.
解答 解:$sinx-cosx=\sqrt{2}sin(x-\frac{π}{4})≤\sqrt{2}$,故①对;
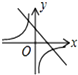
画出函数y=2x,y=x2的图象如下图,
可知②对;
圆x2+y2=4的圆心(0,0)到4x+3y-10=0的距离d=$\frac{|-10|}{\sqrt{{4}^{2}+{3}^{2}}}$=2,
故?(x,y)∈{(x,y)|4x+3y-10=0},均有x2+y2≥4,
故③正确,
因为$A+B<\frac{π}{2}$,
故$\frac{π}{2}>\frac{π}{2}-B>A>0$,
所以1>cosB>sinA>0,
又因为f(x)在(0,1)上单调递减.
故f(sinA)>f(cosB),即④正确;
故真命题的序号有:①②③④,
故答案为:①②③④.
点评 本题以命题的真假判断为载体,考查了三角函数的值域,函数的图象,点到直线距离公式,点与圆的位置关系,函数的单调性等知识点,难度中档.

练习册系列答案
相关题目
11.已知Πn是正项等比数列{an}的前n项积,且满足a7>1,a8<1,则下列结论正确的是( )
| A. | Π7<Π8 | B. | Π15<Π16 | C. | Π13>1 | D. | Π14>1 |
12.记等差数列的前n项和为Sn,若S3=6,S5=25,则该数列的公差d=( )
| A. | 2 | B. | 3 | C. | 6 | D. | 7 |