题目内容
8．已知k，b∈R，则一次函数y=kx+b与反比例函数$y=\frac{kb}{x}$在同一坐标系中的图象可以是（ ）| A． |  | B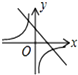． |  | C． |  | D． |  |
分析 通过K的讨论，判断函数的图象即可．
解答 解：当k＜0，b＜0时，一次函数y=kx+b的图象，反比例函数$y=\frac{kb}{x}$，A、B、C、D不成立．
当k＜0，b＞0，一次函数y=kx+b的图象，反比例函数$y=\frac{kb}{x}$，A不成立，B成立，C、D不成立．
当k＞0，b＜0时，一次函数y=kx+b的图象，反比例函数$y=\frac{kb}{x}$，A、B、C、D不成立．
当k＞0，b＞0时，一次函数y=kx+b的图象，反比例函数$y=\frac{kb}{x}$，A、B、C、D不成立．
当k＜0，b＞0，一次函数y=kx+b的图象，反比例函数$y=\frac{kb}{x}$，B成立；
故选：B．
点评 本题考查直线方程与反比例函数图象的判断，考查计算能力．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
15．在等差数列{an}中，对任意n∈N+，都有an＞an+1，且a2，a8是方程x2-12x+m=0的两根，且前15项的和S15=m，则数列{an}的公差是（ ）
| A． | -2或-3 | B． | 2或3 | C． | -2 | D． | -3 |
16．若函数f（x）=$\sqrt{3}$sin（x+φ）-cos（x+φ）（0＜φ＜π）为奇函数，将函数f（x）图象上所有点横坐标变为原来的一半，纵坐标不变；再向右平移$\frac{π}{8}$个单位得到函数g（x），则g（x）的解析式可以是（ ）
| A． | $g（x）=2sin（2x-\frac{π}{4}）$ | B． | $g（x）=2sin（2x-\frac{π}{8}）$ | C． | $g（x）=2sin（\frac{1}{2}x-\frac{π}{4}）$ | D． | $g（x）=2sin（\frac{1}{2}x-\frac{π}{16}）$ |
20．设集合A={x|x2-x-2≤0}，集合B={x|1＜x≤3}，则A∪B=（ ）
| A． | {x|-1≤x≤3} | B． | {x|-1≤x＜1} | C． | {x|1≤x≤2} | D． | {x|2＜x≤3} |