Question

【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BCD=135°，侧面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E、F分别为BC、AD的中点，点M在线段PD上．

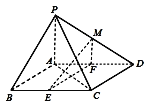
(1)求证：EF⊥平面PAC；

(2)如果直线ME与平面PBC所成的角和直线ME与平

面ABCD所成的角相等，求的值．

Answer 1

【答案】(1)见解析;(2) .

【解析】试题分析： 由平行四边形的性质可得，即，由面面垂直的性质得出平面，故，从而平面

以为原点建立空间直角坐标系，设， ，求出平面，平面的法向量以及的坐标，根据线面角相等列方程求解即可得到答案

解析：(1）证明：在平行四边形中，因为，，

所以．由分别为的中点，得， 所以．

因为侧面底面，且，所以底面．

又因为底面，所以．

又因为，平面，平面，所以平面．

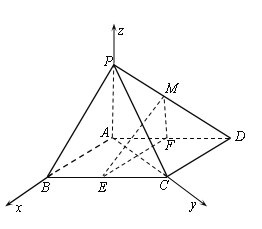
（2）解：因为底面，，所以两两

垂直，以分别为、、，建立空间直角坐标系，则

，

所以，，，

设，则，

所以，，易得平面

的法向量．

设平面的法向量为，由，，得 令， 得．

因为直线与平面所成的角和此直线与平面所成的角相等，

所以，即，所以 ，

解得，或（舍）． 综上所得：