题目内容
4.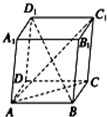 如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
分析 设出空间中的一组基底,把$\overrightarrow{A{C}_{1}}$ 用基底表示,得到$|\overrightarrow{A{C}_{1}}|$与$|\overrightarrow{AB}|$的关系得答案.
解答 解:记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,$\overrightarrow{A{A_1}}=\overrightarrow c$,且$|\overrightarrow a|=|\overrightarrow b|=|\overrightarrow c|=k$,
则$<\overrightarrow a,\overrightarrow b>=<\overrightarrow{b,}\overrightarrow c>=<\overrightarrow c,\overrightarrow a>={60°}$,∴$\overrightarrow{a}•\overrightarrow{b}=\overrightarrow{b}•\overrightarrow{c}=\overrightarrow{c}•\overrightarrow{a}=k•k•cos60°=\frac{1}{2}{k}^{2}$;
∴$|\overrightarrow{A{C}_{1}}{|}^{2}$=$(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})^{2}=|\overrightarrow{a}{|}^{2}+|\overrightarrow{b}{|}^{2}+|\overrightarrow{c}{|}^{2}$$+2\overrightarrow{a}•\overrightarrow{b}+2\overrightarrow{a}•\overrightarrow{c}+2\overrightarrow{b}•\overrightarrow{c}$=$3{k^2}+2(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}){k^2}=6{k^2}$,
∴$|\overrightarrow{A{C_1}}|=\sqrt{6}k$,即$A{C_1}=\sqrt{6}k$;
$AB=|\overrightarrow{AB}|=|\overrightarrow a|=k$,
∴$λ=\frac{{A{C_1}}}{AB}=\frac{{\sqrt{6}k}}{k}=\sqrt{6}$,
故选:A.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力.灵活运用向量求解减少了计算量,是中档题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
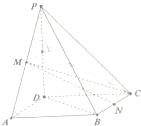 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.