题目内容
14.从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换后,甲在乙左边的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
分析 从左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,则经过两次这样的调换,基本事件总数为n=9,经过两次这样的调换后,甲在乙左边包含的基本事件个数m=6,由此能求出经过两次这样的调换后,甲在乙左边的概率.
解答 解:从左至右依次站着甲、乙、丙3个人,
从中随机抽取2个人进行位置调换,则经过两次这样的调换,
基本事件总数为n=${C}_{3}^{2}•{C}_{3}^{2}$=9,
左至右依次站着甲、乙、丙3个人,从中随机抽取2个人进行位置调换,
第一次调换后,对后的位置关系有三种:
甲丙乙、乙甲丙、丙乙甲,
第二次调换后甲在乙左边对应的关系有:$甲丙乙\left\{\begin{array}{l}{甲乙丙}\\{丙甲乙}\end{array}\right.$,$乙甲丙\left\{\begin{array}{l}{丙甲乙}\\{甲乙丙}\end{array}\right.$,
,丙乙甲$\left\{\begin{array}{l}{甲丙乙}\\{丙甲乙}\end{array}\right.$,
∴经过两次这样的调换后,甲在乙左边包含的基本事件个数m=6,
∴经过两次这样的调换后,甲在乙左边的概率:P=$\frac{6}{9}$=$\frac{2}{3}$,
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
4.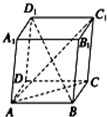 如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
 如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
19.执行如图所示的程序框图,则输出的S的值为( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
4.为了缓解城市拥堵,某市对非居民区的公共停车场制定了不同的收费标准(见表).
如果小王某次停车3小时,缴费24元,请你判断小王该次停车所在地区的类别是( )
| 地区类别 | 首小时内 | 首小时外 |
| 一类 | 2.5元/15分钟 | 3.75元/15分钟 |
| 二类 | 1.5元/15分钟 | 2.25元/15分钟 |
| 三类 | 0.5元/15分钟 | 0.75元/15分钟 |
| A. | 一类 | B. | 二类 | C. | 三类 | D. | 无法判断 |
 长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).