Question

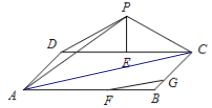
【题目】如图，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.点E是CD边的中点，点F，G分别在线段AB，BC上，且AF＝2FB，CG＝2GB.

(1)证明：PE⊥FG；

(2)求二面角PADC的正切值；

(3)求直线PA与直线FG所成角的余弦值．

Answer 1

【答案】（1）见解析；（2）；（3）．

【解析】试题分析：（1）通过△POC为等腰三角形可得PE⊥CD，利用线面垂直判定定理及性质定理即得结论；

（2）通过（1）及面面垂直定理可得PG⊥AD，则∠PDC为二面角P﹣AD﹣C的平面角，利用勾股定理即得结论；

（3）连结AC，利用勾股定理及已知条件可得FG∥AC，在△PAC中，利用余弦定理即得直线PA与直线FG所成角即为直线PA与直线FG所成角∠PAC的余弦值．

（1）证明：在△POC中PO=PC且E为CD中点，

∴PE⊥CD，

又∵平面PDC⊥平面ABCD，平面PDC∩平面ABCD=CD，PE平面PCD，

∴PE⊥平面ABCD，

又∵FG平面ABCD，

∴PE⊥FG；

（2）解：由（1）知PE⊥平面ABCD，∴PE⊥AD，

又∵CD⊥AD且PE∩CD=E，

∴AD⊥平面PDC，

又∵PD平面PDC，∴AD⊥PD，

又∵AD⊥CD，∴∠PDC为二面角P﹣AD﹣C的平面角，

在Rt△PDE中，由勾股定理可得：

PE===，

∴tan∠PDC==；

（3）解：连结AC，则AC==3，

在Rt△ADP中，AP===5，

∵AF=2FB，CG=2GB，

∴FG∥AC，

∴直线PA与直线FG所成角即为直线PA与直线FG所成角∠PAC，

在△PAC中，由余弦定理得

cos∠PAC=

=

=．