题目内容
【题目】若函数![]() 在定义域内存在实数x,满足
在定义域内存在实数x,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
![]() 已知函数
已知函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
![]() 设
设![]() 是定义在
是定义在![]() 上的“局部奇函数”,求实数m的取值范围;
上的“局部奇函数”,求实数m的取值范围;
![]() 若
若![]() 为定义域R上的“局部奇函数”,求实数m的取值范围.
为定义域R上的“局部奇函数”,求实数m的取值范围.
【答案】(1)是“局部奇函数”;(2)![]() ;(3)
;(3)![]() .
.
【解析】
![]() 运用两角和与差的正弦公式,化简
运用两角和与差的正弦公式,化简![]() ,再由由局部奇函数的定义,即可判断;
,再由由局部奇函数的定义,即可判断;
![]() 根据局部奇函数的定义,可得方程
根据局部奇函数的定义,可得方程![]() 在
在![]() 上有解,运用换元法,令
上有解,运用换元法,令![]() ,则
,则![]() ,求出右边的值域即可;
,求出右边的值域即可;
![]() 根据“局部奇函数”的定义可知,
根据“局部奇函数”的定义可知,![]() 有解即可
有解即可![]() 设
设![]() ,则
,则![]() ,即有方程等价为
,即有方程等价为![]() 在
在![]() 时有解,设
时有解,设![]() ,由对称轴和区间的关系,列出不等式,解出即可.
,由对称轴和区间的关系,列出不等式,解出即可.
解:![]() 由于
由于![]() ,
,![]() ,
,
则![]() ,由于
,由于![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 成立,由局部奇函数的定义,可知该函数
成立,由局部奇函数的定义,可知该函数![]() 为“局部奇函数”;
为“局部奇函数”;
![]() 根据局部奇函数的定义,
根据局部奇函数的定义,![]() 时,
时,![]() 可化为
可化为![]() ,
,
因为![]() 的定义域为
的定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 上有解,
上有解,
令![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为减函数,
上为减函数,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() 时,
时,![]() 所以
所以![]() ,
,
即![]() .
.
![]() 根据“局部奇函数”的定义可知,函数
根据“局部奇函数”的定义可知,函数![]() 有解即可,
有解即可,
即![]() ,
,
![]() ,
,
即![]() 有解即可.
有解即可.
设![]() ,则
,则![]() ,
,
![]() 方程等价为
方程等价为![]() 在
在![]() 时有解,
时有解,
设![]() ,
,
对称轴![]() ,
,
![]() 若
若![]() ,则
,则![]() ,
,
即![]() ,
,
![]() ,此时
,此时![]() ,
,
![]() 若
若![]() ,要使
,要使![]() 在
在![]() 时有解,
时有解,
则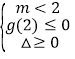 ,即
,即 ,
,
解得![]() ,
,
综上得,![]()

【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价x和销售量y之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量(件) | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中![]() ,
,![]()
【题目】某单位为促进职工业务技能提升,对该单位120名职工进行一次业务技能测试,测试项目共5项.现从中随机抽取了10名职工的测试结果,将它们编号后得到它们的统计结果如下表(表1)所示(“√”表示测试合格,“×”表示测试不合格).
表1:
编号\测试项目 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
规定:每项测试合格得5分,不合格得0分.
(1)以抽取的这10名职工合格项的项数的频率代替每名职工合格项的项数的概率.
①设抽取的这10名职工中,每名职工测试合格的项数为![]() ,根据上面的测试结果统计表,列出
,根据上面的测试结果统计表,列出![]() 的分布列,并估计这120名职工的平均得分;
的分布列,并估计这120名职工的平均得分;
②假设各名职工的各项测试结果相互独立,某科室有5名职工,求这5名职工中至少有4人得分不少于20分的概率;
(2)已知在测试中,测试难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 项测试难度,
项测试难度,![]() 为第
为第![]() 项合格的人数,
项合格的人数,![]() 为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
为参加测试的总人数.已知抽取的这10名职工每项测试合格人数及相应的实测难度如下表(表2):
表2:
测试项目 | 1 | 2 | 3 | 4 | 5 |
实测合格人数 | 8 | 8 | 7 | 7 | 2 |
定义统计量![]() ,其中
,其中![]() 为第
为第![]() 项的实测难度,
项的实测难度,![]() 为第
为第![]() 项的预测难度(
项的预测难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
,则称该次测试的难度预测合理,否则为不合理,测试前,预估了每个预测项目的难度,如下表(表3)所示:
表3:
测试项目 | 1 | 2 | 3 | 4 | 5 |
预测前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
判断本次测试的难度预估是否合理.