题目内容
【题目】已知函数![]() .
.
(Ⅰ)求f(x)的最小正周期和单调增区间;
(Ⅱ)当x∈[﹣![]() ,
,![]() ]时,求函数f(x)的最小值和最大值.
]时,求函数f(x)的最小值和最大值.
【答案】(Ⅰ)最小正周期为![]() ,单调增区间为
,单调增区间为![]() ;(Ⅱ)最小值和最大值分别为
;(Ⅱ)最小值和最大值分别为![]() 和0
和0
【解析】
(Ⅰ)利用二倍角的余弦公式以及两角和与差的正弦公式将函数![]() 化为
化为![]() ,利用正弦函数的周期公式可得函数的周期,利用正弦函数的单调性解不等式,可得到函数
,利用正弦函数的周期公式可得函数的周期,利用正弦函数的单调性解不等式,可得到函数![]() 的递增区间;(Ⅱ)由
的递增区间;(Ⅱ)由![]() 可得
可得![]() ,结合正弦函数的单调性即可得结果.
,结合正弦函数的单调性即可得结果.
(Ⅰ)化简可得![]()
=![]() sin2x﹣
sin2x﹣![]() (1+cos2x)﹣
(1+cos2x)﹣![]()
=![]() sin2x﹣
sin2x﹣![]() cos2x﹣1
cos2x﹣1
=sin(2x﹣![]() )﹣1,
)﹣1,
∴f(x)的最小正周期T=![]() =π,
=π,
由2kπ﹣![]() ≤2x﹣
≤2x﹣![]() ≤2kπ+
≤2kπ+![]() 可得kπ﹣
可得kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]()
∴函数的单调增区间为[kπ﹣![]() ,kπ+
,kπ+![]() ]k∈Z;
]k∈Z;
(Ⅱ)当x∈[﹣![]() ,
,![]() ]时,2x﹣
]时,2x﹣![]() ∈[﹣
∈[﹣![]() ,
,![]() ],
],
∴sin(2x﹣![]() )∈[﹣
)∈[﹣![]() ,1],
,1],
∴函数f(x)的最小值和最大值分别为﹣![]() ﹣1和0.
﹣1和0.

【题目】天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:![]() 。
。
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
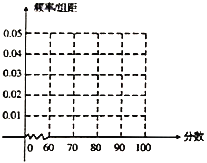
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.