Question

【题目】已知数列的前项和满足：（为常数，且，）．

（1）求的通项公式；

（2）设，若数列为等比数列，求的值；

（3）在满足条件（2）的情形下，设，数列的前项和为，若不等式对任意的恒成立，求实数的取值范围．

Answer 1

【答案】（1）（2）（3）

【解析】

试题分析：（1）由与关系求通项，注意分类讨论：当时，，得．当时，由，相减得，因此是等比数列，且公比是，所以（2）先代入化简得，由数列为等比数列得，解得，最后验证（3）先求前项和为，代入化简不等式得，所以只需求最大值，利用相邻两项关系求数列单调性，确定最大值

试题解析：解：（1）当时，，得．

当时，由，即，①

得，②

①②，得，即，∴（），

∴是等比数列，且公比是，∴．

（2）由（1）知，，即，

若数列为等比数列，则有，

而，，，

故，解得，

再将代入，得，

由，知为等比数列，∴．

（3）由，知，∴，

∴，

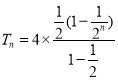
由不等式恒成立，得恒成立，

设，由，

∴当时，，当时，，

而，，∴，

∴，∴．