题目内容
【题目】已知函数![]() ,
,![]() ,且函数
,且函数![]() 是偶函数.
是偶函数.
(1)求![]() 的解析式;.
的解析式;.
(2)若不等式![]() 在
在![]() 上恒成立,求n的取值范围;
上恒成立,求n的取值范围;
(3)若函数 恰好有三个零点,求k的值及该函数的零点.
恰好有三个零点,求k的值及该函数的零点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,该函数的零点为0,
,该函数的零点为0,![]() ,2.
,2.
【解析】
(1)根据![]() 是偶函数求得表达式算出
是偶函数求得表达式算出![]() 的值,进而求得
的值,进而求得![]() 的解析式即可.
的解析式即可.
(2)换元令![]() ,再求解
,再求解![]() 的最小值,化简利用二次不等式进行范围运算即可.
的最小值,化简利用二次不等式进行范围运算即可.
(3)换元令![]() ,结合复合函数的零点问题,分析即可.
,结合复合函数的零点问题,分析即可.
(1)∵![]() ,
,
∴![]() .
.
∵![]() 是偶函数,∴
是偶函数,∴![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]() .
.
(2)令![]() ,∵
,∵![]() ,
,
∴![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立,
上恒成立,
∴
令![]() ,
,![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
(3)令![]() ,则
,则![]() ,方程
,方程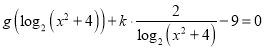 可化为
可化为![]() ,即
,即![]() ,也即
,也即![]() .
.
又∵方程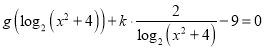 有三个实数根,
有三个实数根,
∴![]() 有一个根为2,∴
有一个根为2,∴![]() .
.
∴![]() ,解得
,解得![]() 或
或![]() .
.
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,∴该函数的零点为0,-2,2.
,∴该函数的零点为0,-2,2.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目