题目内容
【题目】定义:对棱相等的四面体为等腰四面体.
(1)若等腰四面体的每条棱长都是![]() ,求该等腰四面体的体积;
,求该等腰四面体的体积;
(2)求证:等腰四面体每个面的三角形均为锐角三角形:
(3)设等腰四面体![]() 的三个侧面与底面所成的角分别为
的三个侧面与底面所成的角分别为![]() ,请判断
,请判断![]() 是否为定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
是否为定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
【答案】(1)![]() (2)证明见解析;(3)是定值;定值为1
(2)证明见解析;(3)是定值;定值为1
【解析】
由条件,四面体的对棱相等,则可以将四面体放到长方体中去.
(1)当等腰四面体的每条棱长都是![]() 时,长方体是正方体,且正方体的棱长为
时,长方体是正方体,且正方体的棱长为![]() ,该等腰四面体的体积为正方体的体积减去4个角上的4个全等的小三棱锥的体积,则可求出答案.
,该等腰四面体的体积为正方体的体积减去4个角上的4个全等的小三棱锥的体积,则可求出答案.
(2)设长方体的长、宽、高分别为![]() ,在该四面体的每个面中,任意两边的平方之和都大于第三边的平方,从而可证.
,在该四面体的每个面中,任意两边的平方之和都大于第三边的平方,从而可证.
(3)过![]() 作
作![]() 平面
平面![]() 交平面
交平面![]() 于点
于点![]() ,
,![]() 为面
为面![]() 与底面
与底面![]() 所成的角,
所成的角,  ,根据题意设
,根据题意设![]() ,面
,面![]() 与底面
与底面![]() 所成的角分别为
所成的角分别为![]() ,同理可得:
,同理可得:![]() ,又
,又![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() ,从而可得答案.
,从而可得答案.
由条件,四面体的对棱相等,则可以将四面体放到长方体中去,如图.
(1)当等腰四面体的每条棱长都是![]() 时,长方体是正方体,且正方体的棱长为
时,长方体是正方体,且正方体的棱长为![]() .
.
此时该等腰四面体的体积为正方体的体积减去4个角上的4个全等的小三棱锥的体积.
所以![]() .
.
(2)设长方体的长、宽、高分别为![]() .
.
则![]() ,
,![]() ,
,![]() .
.
在面![]() 中,
中,
所以![]() 为锐角.
为锐角.
同理:在该四面体的每个面中,任意两边的平方之和都大于第三边的平方.
根据余弦定理可得,每个面中的三角形均为锐角三角形.
所以等腰四面体每个面的三角形均为锐角三角形.
(3) ![]() 的值为定值1.
的值为定值1.
过![]() 作
作![]() 平面
平面![]() 交平面
交平面![]() 于点
于点![]() ,则
,则![]()
过![]() 作
作![]() 交
交![]() 于
于![]() ,所以
,所以![]() 平面
平面![]() ,则
,则![]() .
.
所以![]() 为面
为面![]() 与底面
与底面![]() 所成的角,设
所成的角,设![]()

设面![]() 与底面
与底面![]() 所成的角分别为
所成的角分别为![]() .
.
同理可得:![]()
又![]() ≌
≌![]() ≌
≌![]() ≌
≌![]()
 .
.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(GB/T19522-2010)》于2011年7月1日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,且图表示的函数模型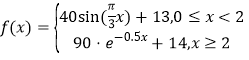 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
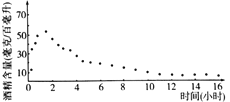
喝1瓶啤酒的情况
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某钢铁加工厂新生产一批钢管,为了了解这批产品的质量状况,检验员随机抽取了![]() 件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
|
|
|
| ||
|
| |
| ||
| ||
|
|
|
|
|
|
合计 |
|
|

(1)求![]() ,
,![]() ;
;
(2)根据质量标准规定:钢管内径尺寸大于等于![]() 或小于
或小于![]() 为不合格,钢管内径尺寸在
为不合格,钢管内径尺寸在![]() 或
或![]() 为合格,钢管内径尺寸在
为合格,钢管内径尺寸在![]() 为优等.钢管的检测费用为
为优等.钢管的检测费用为![]() 元/根,把样本的频率分布作为这批钢管的概率分布.
元/根,把样本的频率分布作为这批钢管的概率分布.
(i)若从这批钢管中随机抽取![]() 根,求内径尺寸为优等钢管根数
根,求内径尺寸为优等钢管根数![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)已知这批钢管共有![]() 根,若有两种销售方案:
根,若有两种销售方案:
第一种方案:不再对该批剩余钢管进行检测,扣除![]() 根样品中的不合格钢管后,其余所有钢管均以
根样品中的不合格钢管后,其余所有钢管均以![]() 元/根售出;
元/根售出;
第二种方案:对该批钢管进行一一检测,不合格钢管不销售,并且每根不合格钢管损失![]() 元,合格等级的钢管
元,合格等级的钢管![]() 元/根,优等钢管
元/根,优等钢管![]() 元/根.
元/根.
请你为该企业选择最好的销售方案,并说明理由.
【题目】疫情期间,有一批货物需要用汽车从城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
所用时间 | 10 | 11 | 12 | 13 |
通过公路1的频数 | 20 | 40 | 20 | 20 |
通过公路2的频数 | 10 | 40 | 40 | 10 |
(1)为进行某项研究,从所用时间为12的60辆汽车中随机抽取6辆,若用分层随机抽样的方法抽取,求从通过公路1和公路2的汽车中各抽取几辆:
(2)若从(1)的条件下抽取的6辆汽车中,再任意抽取2辆汽车,求这2辆汽车至少有1辆通过公路1的概率;
(3)假设汽车A只能在约定时间的前11h出发,汽车B只能在约定时间的前12h出发.为了尽最大可能在各自允许的时间内将货物从城市甲运到城市乙,汽车A和汽车B应如何选择各自的道路?
