题目内容
【题目】如图,四边形![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]() 平面
平面![]() ,且
,且![]() .
.
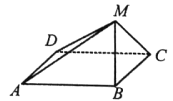
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当![]() ,且
,且![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() 时,求二面角
时,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)由已知条件和面面垂直性质定理可以证得![]() 平面
平面![]() ,有
,有![]() ,再运用面面垂直的判定定理证明平面
,再运用面面垂直的判定定理证明平面![]() 平面
平面![]()
(2)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向建立直角坐标系
轴正方向建立直角坐标系![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,运用公式求出二面角夹角的余弦值,继而求出正弦值
的法向量,运用公式求出二面角夹角的余弦值,继而求出正弦值
(1)由题设知,平面![]() 平面
平面![]() ,交线为
,交线为![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因此![]() ,又
,又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向建立如图所示的直角坐标系
轴正方向建立如图所示的直角坐标系![]() ,
,

则有![]() ,
,
过点![]() 作
作![]() 于
于![]() ,设
,设![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() ,
,
由题设可得![]() ,即
,即![]() ,
,
![]() 解得
解得![]() 或
或![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() .
.
由![]() ,知
,知![]() 是平面
是平面![]() 的法向量,
的法向量,
![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则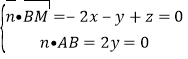 取
取![]() 得
得![]() ,
,
设二面角![]() 为
为![]() ,
,
则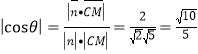 ,
,
因为![]() ,
,
![]() .
.
综上,二面角![]() 的正弦值为
的正弦值为![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】某班主任对全班50名学生进行了作业量多少的调查,喜欢玩电脑游戏的同学认为作业多的有18人,认为作业不多的有9人,不喜欢玩电脑游戏的同学认为作业多的有8人,认为作业不多的有15人,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约是多少?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(GB/T19522-2010)》于2011年7月1日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,且图表示的函数模型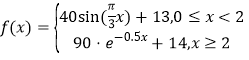 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
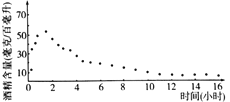
喝1瓶啤酒的情况
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】某钢铁加工厂新生产一批钢管,为了了解这批产品的质量状况,检验员随机抽取了![]() 件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
|
|
|
| ||
|
| |
| ||
| ||
|
|
|
|
|
|
合计 |
|
|

(1)求![]() ,
,![]() ;
;
(2)根据质量标准规定:钢管内径尺寸大于等于![]() 或小于
或小于![]() 为不合格,钢管内径尺寸在
为不合格,钢管内径尺寸在![]() 或
或![]() 为合格,钢管内径尺寸在
为合格,钢管内径尺寸在![]() 为优等.钢管的检测费用为
为优等.钢管的检测费用为![]() 元/根,把样本的频率分布作为这批钢管的概率分布.
元/根,把样本的频率分布作为这批钢管的概率分布.
(i)若从这批钢管中随机抽取![]() 根,求内径尺寸为优等钢管根数
根,求内径尺寸为优等钢管根数![]() 的分布列和数学期望;
的分布列和数学期望;
(ii)已知这批钢管共有![]() 根,若有两种销售方案:
根,若有两种销售方案:
第一种方案:不再对该批剩余钢管进行检测,扣除![]() 根样品中的不合格钢管后,其余所有钢管均以
根样品中的不合格钢管后,其余所有钢管均以![]() 元/根售出;
元/根售出;
第二种方案:对该批钢管进行一一检测,不合格钢管不销售,并且每根不合格钢管损失![]() 元,合格等级的钢管
元,合格等级的钢管![]() 元/根,优等钢管
元/根,优等钢管![]() 元/根.
元/根.
请你为该企业选择最好的销售方案,并说明理由.