Question

【题目】已知函数f（x）=Acos（ωx+α）（A＞0，ω＞0，0＜α＜π）为奇函数，该函数的部分图象如图所示，△EFG是边长为2的等边三角形，则f（1）的值为 ．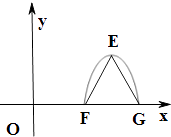

Answer 1

【答案】-
【解析】解：∵f（x）=Acos（ωx+φ）为奇函数，∴f（0）=Acosφ=0．
∵0＜φ＜π，∴φ= ，∴f（x）=Acos（ωx+ ）=﹣Asinωx，
∵△EFG是边长为2的等边三角形，则yE= =A，
又∵函数的周期 T=2FG=4，根据周期公式可得，ω= = ，
∴f（x）=﹣Asin x=﹣ sin x，则f（1）=﹣ ，
所以答案是：﹣ ．
【考点精析】本题主要考查了函数的值的相关知识点，需要掌握函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法才能正确解答此题．