题目内容
【题目】如图,四棱锥![]() 的侧面
的侧面![]() 是正三角形,底面
是正三角形,底面![]() 是直角梯形,
是直角梯形,![]() .
.
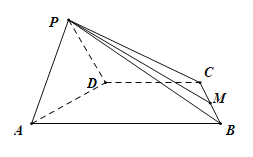
(1)求证:![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 中点
中点![]() ,根据等边三角形性质得
,根据等边三角形性质得![]() ,根据直角梯形以及中位线得
,根据直角梯形以及中位线得![]() ,最后根据线面垂直判定定理以及性质定理证得结果;
,最后根据线面垂直判定定理以及性质定理证得结果;
(2)解法一,建立空间直角坐标系,先求平面![]() 一个法向量,再根据向量数量积求向量夹角,最后根据线面角与向量夹角关系得结果;
一个法向量,再根据向量数量积求向量夹角,最后根据线面角与向量夹角关系得结果;
解法二,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用平行转化求点
,利用平行转化求点![]() 到平面
到平面![]() 的距离,过点
的距离,过点![]() 作
作![]() ,可证
,可证![]() 平面
平面![]() ,再根据直角三角形求得结果.
,再根据直角三角形求得结果.
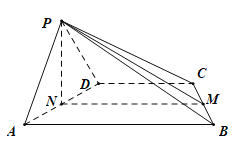
(1)证明:取![]() 中点
中点![]() ,连
,连![]() ,
,![]() ,
,
因为![]() 是正三角形,所以
是正三角形,所以![]() ,
,
又![]() 是
是![]() 中点,所以
中点,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() .
.
(2)![]() ,又
,又![]() ,所以
,所以![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
由定理可知![]() 平面
平面![]() ,
,
建立如图所示的空间直角坐标系,不妨设![]() ,
,
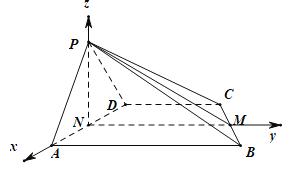
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
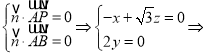 可取
可取![]() ,
,
又![]() ,
,
所以,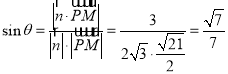 .
.
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
解法二:
![]() ,又
,又![]() ,所以
,所以![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
由定理可知![]() 平面
平面![]() ,不妨设
,不妨设![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,点
,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,故点
,故点![]() 到平面
到平面![]() 的距离也为
的距离也为![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,由定理即知
,由定理即知![]() 平面
平面![]() ,
,
在![]() 中,
中,![]() ,
,
所以,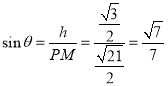 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 |
|
|
|
|
|
|
|
年利润增长 |
|
|
|
|
|
|
|
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为
的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为![]() 万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
(2)现从2012年—2018年这![]() 年中抽出三年进行调查,记
年中抽出三年进行调查,记![]() 年利润增长
年利润增长![]() 投资金额,设这三年中
投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: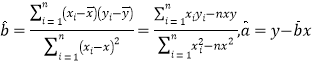 .
.
参考数据:![]() ,
,![]() .
.
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
