题目内容
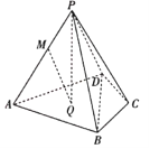
【题目】如图在四棱锥![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,Q为四边形
,Q为四边形![]() 的外接圆的圆心,
的外接圆的圆心,![]() 平面
平面![]() ,M在棱
,M在棱![]() 上,且
上,且![]() .
.
(1)证明:![]() 平面
平面![]() .
.
(2)若![]() 与平面
与平面![]() 所成角为60°,求
所成角为60°,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1) 连接![]() ,交
,交![]() 于点O,连接
于点O,连接![]() ,再根据三角形中的性质证明
,再根据三角形中的性质证明![]() 即可.
即可.
(2) 根据线面角的性质可得![]() 与平面
与平面![]() 所成角为
所成角为![]() ,再以O为坐标原点的空间直角坐标系
,再以O为坐标原点的空间直角坐标系![]() ,利用空间向量求解
,利用空间向量求解![]() 与平面
与平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
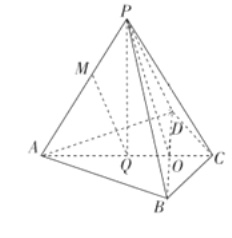
(1)证明:如图,连接![]() ,交
,交![]() 于点O,连接
于点O,连接![]() .
.
∵![]() ,∴
,∴![]() ,则
,则![]() ,
,
∴O为![]() 的中点.
的中点.
∵Q为四边形![]() 的外接圆的圆心,∴Q为等边
的外接圆的圆心,∴Q为等边![]() 的外接圆的圆心,
的外接圆的圆心,
∴Q为等边![]() 的重心,则
的重心,则![]() .
.
又![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:∵![]() 平面
平面![]() ,
,
∴![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则![]() .
.
建立如图所示的以O为坐标原点的空间直角坐标系![]() ,
,
∴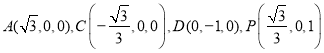 ,
,
∴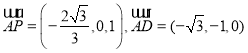 .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即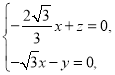
令![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,∵
,∵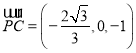 ,
,
∴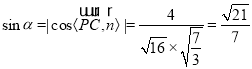 ,
,
∴![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式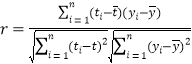
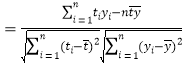 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式: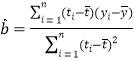
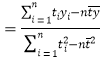 ,
,![]() )
)
【题目】某公司为了提高利润,从2012年至2018年每年对生产环节的改进进行投资,投资金额与年利润增长的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 |
|
|
|
|
|
|
|
年利润增长 |
|
|
|
|
|
|
|
(1)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为
的回归直线方程;如果2019年该公司计划对生产环节的改进的投资金额为![]() 万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
万元,估计该公司在该年的年利润增长为多少?(结果保留两位小数)
(2)现从2012年—2018年这![]() 年中抽出三年进行调查,记
年中抽出三年进行调查,记![]() 年利润增长
年利润增长![]() 投资金额,设这三年中
投资金额,设这三年中![]() (万元)的年份数为
(万元)的年份数为![]() ,求随机变量
,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考公式: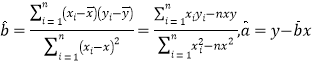 .
.
参考数据:![]() ,
,![]() .
.