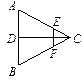题目内容
(本小题满分14分)
如图,在三棱柱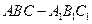 中,侧面
中,侧面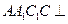 底面ABC,
底面ABC,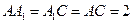 ,
,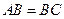 ,且
,且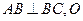 为AC中点。
为AC中点。
(I) 证明: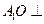 平面ABC;
平面ABC;
(II) 求直线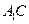 与平面
与平面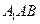 所成角的正弦值;
所成角的正弦值;
(III) 在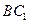 上是否存在一点E,使得
上是否存在一点E,使得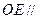 平面
平面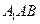 ,若不存在,说明理由;若存在,确定点E的位置。
,若不存在,说明理由;若存在,确定点E的位置。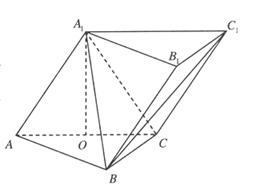
如图,在三棱柱
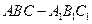 中,侧面
中,侧面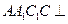 底面ABC,
底面ABC,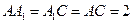 ,
,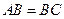 ,且
,且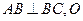 为AC中点。
为AC中点。(I) 证明:
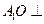 平面ABC;
平面ABC;(II) 求直线
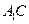 与平面
与平面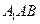 所成角的正弦值;
所成角的正弦值;(III) 在
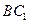 上是否存在一点E,使得
上是否存在一点E,使得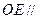 平面
平面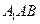 ,若不存在,说明理由;若存在,确定点E的位置。
,若不存在,说明理由;若存在,确定点E的位置。
(Ⅰ)见解析(Ⅱ)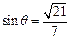 ,(Ⅲ)E为
,(Ⅲ)E为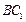 的中点
的中点
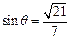 ,(Ⅲ)E为
,(Ⅲ)E为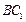 的中点
的中点(Ⅰ)证明:因为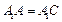 ,且O为AC的中点,
,且O为AC的中点,
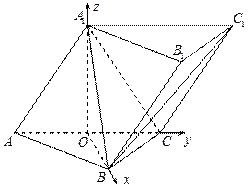
所以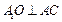 . ………………1分
. ………………1分
又由题意可知,平面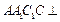 平面
平面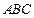 ,交线为
,交线为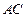 ,且
,且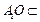 平面
平面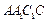 ,
,
所以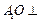 平面
平面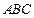 . ………………4分
. ………………4分
(Ⅱ)如图,以O为原点,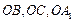 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.
由题意 可知,
可知, 又
又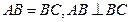
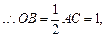
所以得: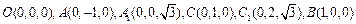
则有: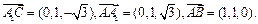 ………………6分
………………6分
设平面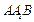 的一个法向量为
的一个法向量为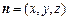 ,则有
,则有
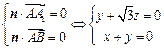 ,令
,令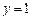 ,得
,得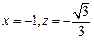
所以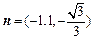 . ………………7分
. ………………7分
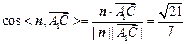 . ………………9分
. ………………9分
因为直线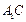 与平面
与平面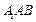 所成角
所成角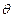 和向量
和向量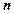 与
与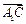 所成锐角互余,所以
所成锐角互余,所以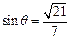 . ………………10分
. ………………10分
(Ⅲ)设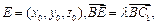 ………………11分
………………11分
即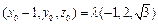 ,得
,得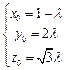
所以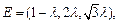 得
得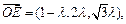 ………………12分
………………12分
令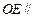 平面
平面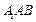 ,得
,得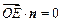 , ………………13分
, ………………13分
即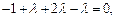 得
得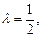
即存在这样的点E,E为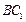 的中点. ………………14分
的中点. ………………14分
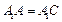 ,且O为AC的中点,
,且O为AC的中点,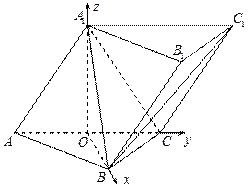
所以
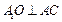 . ………………1分
. ………………1分又由题意可知,平面
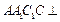 平面
平面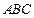 ,交线为
,交线为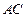 ,且
,且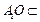 平面
平面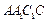 ,
,所以
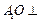 平面
平面 . ………………4分
. ………………4分(Ⅱ)如图,以O为原点,
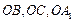 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.由题意
 可知,
可知, 又
又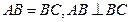
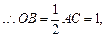
所以得:
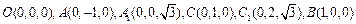
则有:
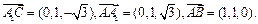 ………………6分
………………6分设平面
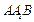 的一个法向量为
的一个法向量为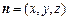 ,则有
,则有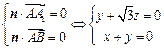 ,令
,令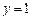 ,得
,得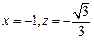
所以
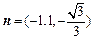 . ………………7分
. ………………7分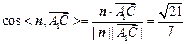 . ………………9分
. ………………9分因为直线
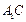 与平面
与平面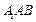 所成角
所成角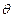 和向量
和向量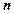 与
与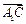 所成锐角互余,所以
所成锐角互余,所以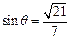 . ………………10分
. ………………10分(Ⅲ)设
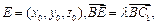 ………………11分
………………11分即
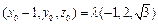 ,得
,得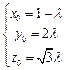
所以
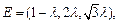 得
得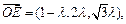 ………………12分
………………12分令
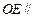 平面
平面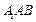 ,得
,得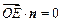 , ………………13分
, ………………13分即
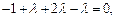 得
得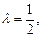
即存在这样的点E,E为
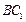 的中点. ………………14分
的中点. ………………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
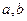 公垂线段
公垂线段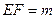 ,线段
,线段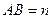 ,
,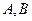 分别在
分别在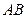 中点轨迹
中点轨迹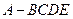 中,底面
中,底面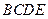 为矩形,侧面
为矩形,侧面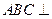 底面
底面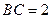 ,
,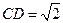 ,
,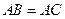 。
。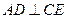 ;
;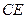 与平面
与平面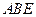 所成的角为
所成的角为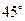 ,求二面角
,求二面角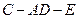 的大小。
的大小。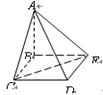
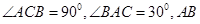 的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)
的垂直平分线分别交AB,AC于E,E(图一),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图二)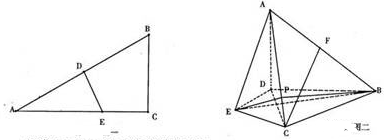
 中,AB=BC=4,
中,AB=BC=4,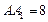 ,E为
,E为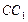 的中点,
的中点,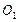 为下底面正方形的中心.求:(I)二面角C—AB—
为下底面正方形的中心.求:(I)二面角C—AB—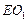 所成角的正切值;
所成角的正切值;
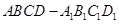 ,的棱长为1,
,的棱长为1,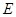 为
为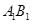 的中点,则下列五个命题:
的中点,则下列五个命题: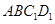 ,的距离为
,的距离为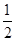
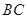 与平面
与平面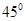
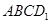 ,在正方体六个面内形成六个射影,其面积的最小值是
,在正方体六个面内形成六个射影,其面积的最小值是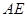 与
与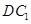 所成的角
所成的角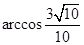
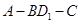 的大小为
的大小为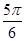
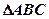 的内角A、B、C所对边的长分别为a、b、c,且
的内角A、B、C所对边的长分别为a、b、c,且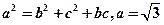 ,球心O到截面ABC的距离为
,球心O到截面ABC的距离为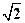 ,则该球的表面积为 。
,则该球的表面积为 。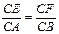 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).