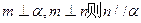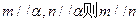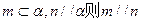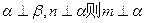题目内容
异面直线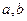 公垂线段
公垂线段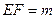 ,线段
,线段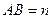 ,
,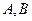 分别在
分别在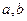 上移动,求
上移动,求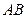 中点轨迹
中点轨迹
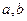 公垂线段
公垂线段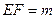 ,线段
,线段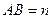 ,
,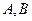 分别在
分别在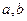 上移动,求
上移动,求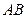 中点轨迹
中点轨迹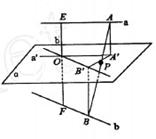 见解析
见解析由立体几何知,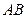 的中点
的中点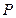 在过
在过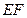 的中点
的中点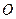 且与
且与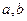 平行的平面
平行的平面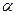 内,取
内,取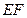 的中点
的中点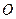 ,过
,过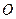 作
作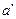 ∥
∥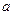 ,
,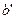 ∥
∥ ,则
,则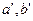 确定平面
确定平面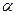 ,
,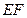
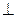
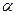 ,则
,则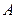 在
在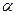 内的射影
内的射影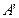 必在
必在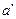 上,
上,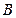 在
在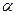 的射影
的射影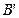 必在
必在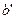 上,
上,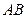 的中点
的中点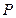 必在
必在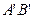 上,如图所示,
上,如图所示,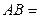
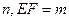 ,易得
,易得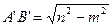 ,
,
现在求线段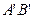 移动时,中点
移动时,中点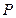 的轨迹。以∠
的轨迹。以∠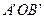 的平分线为
的平分线为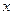 轴,
轴,
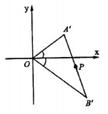
 为坐标原点建立直角坐标系,如图,不妨设
为坐标原点建立直角坐标系,如图,不妨设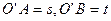
∠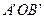
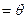 ,在△
,在△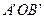 中,由余弦定理得
中,由余弦定理得
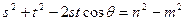 ,设
,设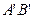 中点坐标为
中点坐标为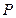
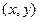 ,则
,则
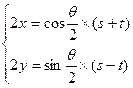 ,得
,得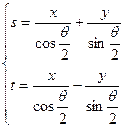 ,代入消去
,代入消去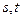 得
得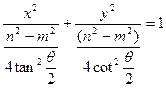
(1) 当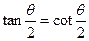 ,即
,即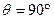 ,两异面直线垂直时,表示圆
,两异面直线垂直时,表示圆
(2) 当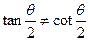 ,即
,即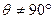 ,两异面直线不垂直时,
,两异面直线不垂直时,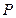 的轨迹是椭圆夹在∠
的轨迹是椭圆夹在∠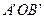 内的弧,同样可以得到椭圆其余弧,故
内的弧,同样可以得到椭圆其余弧,故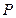 轨迹是
轨迹是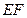 的中垂面上以
的中垂面上以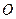 为中心的椭圆
为中心的椭圆
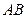 的中点
的中点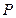 在过
在过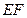 的中点
的中点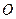 且与
且与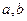 平行的平面
平行的平面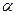 内,取
内,取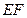 的中点
的中点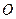 ,过
,过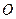 作
作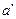 ∥
∥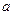 ,
,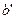 ∥
∥ ,则
,则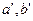 确定平面
确定平面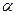 ,
,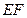
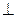
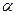 ,则
,则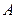 在
在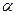 内的射影
内的射影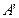 必在
必在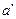 上,
上,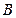 在
在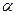 的射影
的射影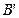 必在
必在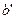 上,
上,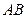 的中点
的中点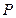 必在
必在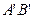 上,如图所示,
上,如图所示,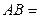
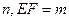 ,易得
,易得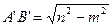 ,
,现在求线段
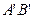 移动时,中点
移动时,中点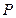 的轨迹。以∠
的轨迹。以∠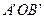 的平分线为
的平分线为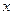 轴,
轴,
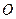 为坐标原点建立直角坐标系,如图,不妨设
为坐标原点建立直角坐标系,如图,不妨设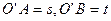
∠
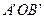
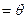 ,在△
,在△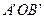 中,由余弦定理得
中,由余弦定理得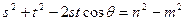 ,设
,设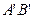 中点坐标为
中点坐标为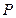
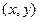 ,则
,则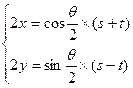 ,得
,得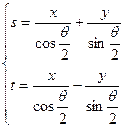 ,代入消去
,代入消去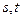 得
得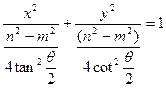
(1) 当
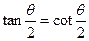 ,即
,即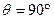 ,两异面直线垂直时,表示圆
,两异面直线垂直时,表示圆(2) 当
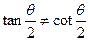 ,即
,即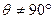 ,两异面直线不垂直时,
,两异面直线不垂直时,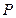 的轨迹是椭圆夹在∠
的轨迹是椭圆夹在∠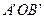 内的弧,同样可以得到椭圆其余弧,故
内的弧,同样可以得到椭圆其余弧,故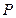 轨迹是
轨迹是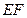 的中垂面上以
的中垂面上以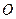 为中心的椭圆
为中心的椭圆
练习册系列答案
相关题目
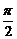 ,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.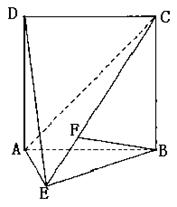
 中,侧面
中,侧面 底面ABC,
底面ABC,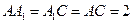 ,
,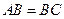 ,且
,且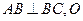 为AC中点。
为AC中点。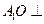 平面ABC;
平面ABC;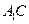 与平面
与平面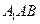 所成角的正弦值;
所成角的正弦值;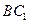 上是否存在一点E,使得
上是否存在一点E,使得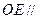 平面
平面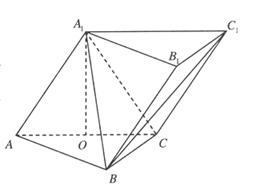
 中,每个侧面均为正方形,
中,每个侧面均为正方形, 为底边
为底边 的中点,
的中点,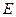 为侧棱
为侧棱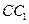 的中点.
的中点.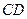 ∥平面
∥平面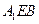 ;
;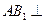 平面
平面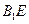 与平面
与平面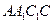 所成角的正弦值.
所成角的正弦值. 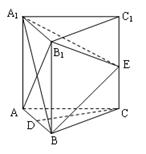
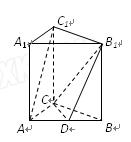
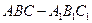 中,
中,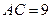 ,
,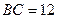
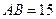 ,
,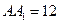 ,点D是
,点D是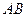 的中点
的中点
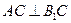 ;
;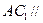 平面
平面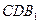 。
。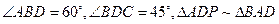 。
。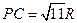 ,求三棱锥P-ABC的体积。
,求三棱锥P-ABC的体积。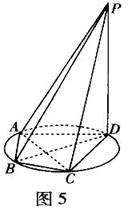
 E是BC的中点。
E是BC的中点。


 ,下列命题中真命题是 ( )
,下列命题中真命题是 ( )