题目内容
4．将正奇数按如图所示的规律排列：则第n（n≥4）行从左向右的第3个数为n2-n+5．
分析 由三角形数阵，知第n行的前面共有1+2+3+…+（n-1）个连续奇数，第n行从左向右的第3个数应为2[$\frac{n（n-1）}{2}$+3]-1．
解答 解：观察三角形数阵，知第n行（n≥3）前共有1+2+3+…+（n-1）=$\frac{n（n-1）}{2}$个连续奇数，
第n行（n≥3）从左向右的第3个数为2[$\frac{n（n-1）}{2}$+3]-1=n2-n+5；
故答案为：n2-n+5．
点评 本题从观察数阵的排列规律，考查了数列的求和应用问题；解题时，关键是发现规律并应用所学知识，来解答问题
练习册系列答案
相关题目
14．若点P的坐标为（x0，y0），曲线C的方程为F（x，y）=0，则“F（x0，y0）=0”是“点P在曲线C上”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
15．设f（x）的定义域为[0，1]，则f（2x-3）的定义域是（ ）
| A． | {x|x≥3} | B． | {x|-2≤x-1} | C． | {x|x≤-2} | D． | {x|log23≤x≤2} |
12．
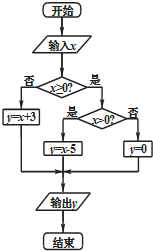执行如图所示的程序框图，在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入，则输出的y值落在区间[-4，3]内的概率为（ ）
执行如图所示的程序框图，在集合A={x∈Z|-9≤x≤10}中随机地取一个数值作为x输入，则输出的y值落在区间[-4，3]内的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |