题目内容
A. [选修4-1:几何证明选讲](本小题满分10分)
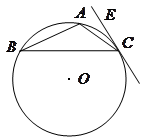
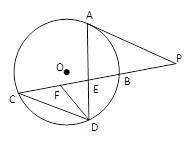
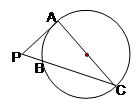
如图,AB是⊙O的直径,C是⊙O外一点,且AC=AB,BC交⊙O于点D.
已知BC=4,AD=6,AC交⊙O于点E,求四边形ABDE的周长.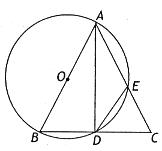
如图,AB是⊙O的直径,C是⊙O外一点,且AC=AB,BC交⊙O于点D.
已知BC=4,AD=6,AC交⊙O于点E,求四边形ABDE的周长.

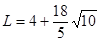
由题意,可由AB是⊙O的直径及AC=AB得出D是中点,由此求得BD,BC的值,再∠DEC=∠B得出∠DEC=∠C,即可求出DE,由图形可得出CE•CA=CD•CB,由此方程解出AE,再求周长即可.
A. [选修4-1:几何证明选讲]
解:AB=AC=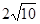
∴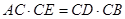 ,则
,则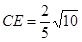
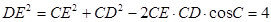 ∴DE=2
∴DE=2
∴四边形ABDE的周长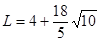
A. [选修4-1:几何证明选讲]
解:AB=AC=
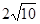
∴
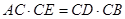 ,则
,则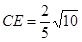
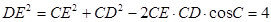 ∴DE=2
∴DE=2∴四边形ABDE的周长
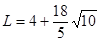

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
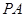 与⊙
与⊙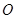 相切,
相切,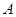 为切点,
为切点,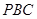 为割线,
为割线,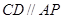 ,
,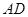 、
、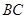 相交于
相交于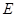 点,
点,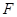 为
为 上一点,且
上一点,且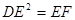 ·
·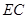 .
.
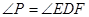 ;
;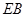 =
=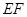 ·
·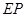 .
.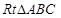 中,
中,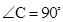 ,
,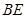 平分
平分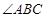 交
交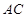 于点
于点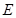 ,点
,点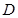 在
在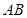 上,
上,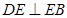 .
.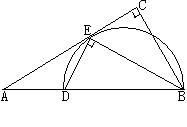
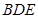 的外接圆的切线;
的外接圆的切线;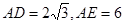 ,求
,求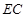 的长.
的长. 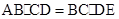
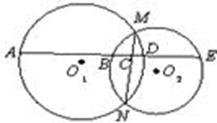
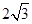 ,AB="BC=4," 则AC的长为
,AB="BC=4," 则AC的长为 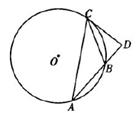
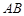 是圆
是圆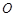 的直径,直线
的直径,直线 与圆
与圆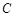 ,
,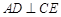 于点
于点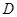 ,若圆
,若圆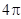 ,
,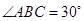 ,则
,则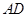 的长为 .
的长为 .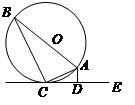
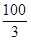 ,它的对角线OB与双曲线
,它的对角线OB与双曲线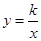 相交于点D,且OB:OD=5:3,则k= .
相交于点D,且OB:OD=5:3,则k= . 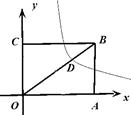
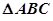 是圆O的内接三角形,圆O的半径
是圆O的内接三角形,圆O的半径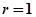 ,
,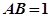 ,
,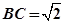 ,
,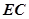 是圆
是圆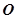 的切线,则
的切线,则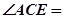 _______.
_______.