题目内容
8.已知正项等差数列{an}的前n项和为Sn,若a1+a2+a3=12,且a22=2a1•(a3+1).(1)求{an}的通项公式;
(2)设b1+b2+…+bn=n•an,求bn.
分析 (1)由已知列方程组求得等差数列的首项和公差,代入通项公式得答案;
(2)把(1)中求得的通项公式代入b1+b2+…+bn=n•an,取n=n-1得另一递推式,作差后求得bn.
解答 解:(1)设等差数列{an}的公差为d,
由a1+a2+a3=12,且a22=2a1•(a3+1),得
$\left\{\begin{array}{l}{3{a}_{1}+3d=12}\\{({a}_{1}+d)^{2}=2{a}_{1}({a}_{1}+2d+1)}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=3}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=0}\\{d=4}\end{array}\right.$(舍),
∴an=1+3(n-1)=3n-2;
(2)由b1+b2+…+bn=n•an,得
b1+b2+…+bn=n•(3n-2)=3n2-2n,
b1+b2+…+bn-1=3(n-1)2-2(n-1)(n≥2),
两式作差得:bn=6n-5(n≥2),
由b1=1适合上式,
∴bn=6n-5.
点评 本题考查等差数列的通项公式,考查由数列的前n项和求数列通项,是中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
16.函数y=4sin(ωx+$\frac{π}{4}$)cos(ωx-$\frac{π}{4}$)-2sin(ωx-$\frac{π}{4}$)•cos(ωx+$\frac{π}{4}$)(ω>0)的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,P4…,且|P3P5|=$\frac{π}{2}$,则此函数的递增区间为( )
| A. | [2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$](k∈Z) | B. | [$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | D. | [$\frac{kπ}{2}$,$\frac{kπ}{2}$+$\frac{π}{4}$](k∈Z) |
18.已知集合A={y|y=x2+1},B={x|y=$\sqrt{4-x}$,(x∈Z)},P=A∩B,则P的真子集的个数为( )
| A. | 14个 | B. | 15个 | C. | 16个 | D. | 17个 |
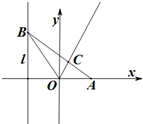 如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.
如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.