题目内容
13.设f(x)=lnx+aex,g(x)=x3-x2-3.(1)求g(x)的单调区间及在x=2处的切线方程l;
(2)若对任意的x∈($\frac{1}{2}$,2),函数y=f(x)的图象都在直线l的下方,求实数a的取值范围.
分析 (1)根据导数和函数的单调性即可求出g(x)的单调区间,再根据导数的几何意义即可求出切线方程;
(2)由于y=8x-15,在x∈($\frac{1}{2}$,2)单调递增,故函数y=f(x)的图象都在直线l的下方,转化为lnx+aex<-11,在x∈($\frac{1}{2}$,2)恒成立,分离参数,构造函数,求出函数的最小值即可.
解答 解:(1)∵g(x)=x3-x2-3,
∴g′(x)=3x2-2x,
令g′(x)=3x2-2x=0解得x=0,或x=$\frac{2}{3}$,
当g′(x)>0时,即x<0,或x>$\frac{2}{3}$,函数单调递增,
当g′(x)<0时,即0<x<$\frac{2}{3}$,函数单调递减,
∴函数g(x)在(-∞,0),或($\frac{2}{3}$,+∞)上单调递增,在(0,$\frac{2}{3}$)上单调递减,
∴g′(2)=3×4-2×2=8,g(2)=8-4-3=1,
∴在x=2处的切线方程l为y-1=8(x-2),即y=8x-15,即8x-y-15=0;
(2)∵对任意的x∈($\frac{1}{2}$,2),函数y=f(x)的图象都在直线l的下方,
∵y=8x-15,在x∈($\frac{1}{2}$,2)单调递增,
∴ymin=8×$\frac{1}{2}$-15=-11,
∴lnx+aex<-11,在x∈($\frac{1}{2}$,2)恒成立,
∴a<-$\frac{11+lnx}{{e}^{x}}$,
设h(x)=-$\frac{11+lnx}{{e}^{x}}$,
∴h′(x)=$\frac{x(11+lnx)-1}{{e}^{x}}$,
令m(x)=11x+xlnx-1,
∴m′(x)=11+lnx>0,在x∈($\frac{1}{2}$,2)恒成立,
∴m(x)>m($\frac{1}{2}$)=$\frac{11}{2}$+$\frac{1}{2}$ln$\frac{1}{2}$-1=$\frac{1}{2}$(9-ln2)>0,
∴h(x)在($\frac{1}{2}$,2)单调递增,
∴h(x)>h($\frac{1}{2}$)=-$\frac{11-ln2}{\sqrt{e}}$=$\frac{ln2-11}{\sqrt{e}}$,
∴a≤$\frac{ln2-11}{\sqrt{e}}$.
点评 本题考查利用导数研究函数的单调性、最值,考查函数恒成立问题,考查转化思想,考查学生分析解决问题的能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 若l∥α,α∩β=m,则l∥m | B. | 若l∥α,m∥α,则l∥m | ||
| C. | 若l⊥α,l∥β,则α⊥β | D. | 若l∥α,l⊥m,则m⊥α |
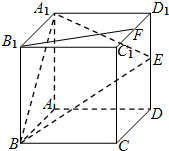 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱DD1、C1D1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是棱DD1、C1D1的中点. 设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$.
设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1、F2,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$.