��Ŀ����
����Ŀ��2012�ꡰ˫�ڡ��ڼ䣬���ٹ�·�����϶�![]() ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij���
ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij���![]() �ֳ����Σ�
�ֳ����Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
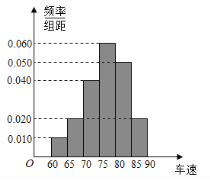
��![]() ��õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
��õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
![]() ij���鹫˾�ڲ����У��õ�����ʲô����������
ij���鹫˾�ڲ����У��õ�����ʲô����������
![]() ����40��С�ͳ������ٵ���������λ���Ĺ���ֵ��
����40��С�ͳ������ٵ���������λ���Ĺ���ֵ��
![]() ���ӳ�����
���ӳ�����![]() �ij������γ�ȡ2����������
�ij������γ�ȡ2����������![]() �ij���������һ���ĸ��ʣ�
�ij���������һ���ĸ��ʣ�
���𰸡���1��ϵͳ��������2�������Ĺ���ֵ����![]() ����λ���Ĺ���ֵΪ
����λ���Ĺ���ֵΪ![]() ����3��
����3��![]() ��
��
��������
![]() �ɳ����ص�ȷ��Ϊϵͳ��������2��ѡ��ֱ��ͼ����ߵľ��������ױߵ��е㼴Ϊ�������������߿�ʼС���ε������Ϊ0.5��Ӧ�ĺ��ἴΪ��λ������3����ͼ�п�֪��������[60��65���ij������ͳ�����[65��70���ij��������ӳ����ڣ�60��70���ij������γ�ȡ2�����賵����[60��65���ij�����Ϊa��b��������[65��70���ij�����Ϊc��d��e��f���г����ԵĻ����¼������Ӷ������Ӧ�ĸ��ʼ��ɣ�
�ɳ����ص�ȷ��Ϊϵͳ��������2��ѡ��ֱ��ͼ����ߵľ��������ױߵ��е㼴Ϊ�������������߿�ʼС���ε������Ϊ0.5��Ӧ�ĺ��ἴΪ��λ������3����ͼ�п�֪��������[60��65���ij������ͳ�����[65��70���ij��������ӳ����ڣ�60��70���ij������γ�ȡ2�����賵����[60��65���ij�����Ϊa��b��������[65��70���ij�����Ϊc��d��e��f���г����ԵĻ����¼������Ӷ������Ӧ�ĸ��ʼ��ɣ�
![]() ������֪��������ǰ������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��һ��������ͬ����ij�������������ĸ����Ƚ϶࣬����һ��ϵͳ������
������֪��������ǰ������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��һ��������ͬ����ij�������������ĸ����Ƚ϶࣬����һ��ϵͳ������
�ʵ��鹫˾�ڲ����У��õ�����ϵͳ������
![]() �����Ĺ���ֵΪ��ߵľ��ε��е㣬�������Ĺ���ֵ����
�����Ĺ���ֵΪ��ߵľ��ε��е㣬�������Ĺ���ֵ����![]() .
.
��ͼ����������Ӧ�ij���Ϊx������λ���Ĺ���ֵΪ��
![]() ��
��
���![]() ������λ���Ĺ���ֵΪ
������λ���Ĺ���ֵΪ![]() ��
��
![]() ��ͼ�п�֪��������
��ͼ�п�֪��������![]() �ij�����Ϊ��
�ij�������![]() ��
��![]() ��
��
������![]() �ij�������
�ij�������![]() ��
��![]() ��
��
�賵����![]() �ij�����Ϊa��b��������
�ij�����Ϊa��b��������![]() �ij�����Ϊc��d��e��f��
�ij�����Ϊc��d��e��f��
�����л����¼��У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��15�֡�
��15�֡�
���г�����![]() �ij���������һ�����¼��У�
�ij���������һ�����¼��У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��14��
��14��
���ԣ�������![]() �ij���������һ���ĸ���Ϊ
�ij���������һ���ĸ���Ϊ![]()

 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д� Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�����Ŀ��ij��λ����10��Ա��������ij����������±���
Ա����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
��н����Ԫ�� | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
��1����õ�λԱ��������н��ƽ��ֵ����λ����
��2����֪Ա����н�����빤����������ع�ϵ��ijԱ��������һ�������������н�ֱ�Ϊ4��Ԫ��5.5��Ԫ��6��Ԫ��8.5��Ԫ��Ԥ���Ա�����������нΪ���٣�
�������Իع鷽��![]() ��ϵ�����㹫ʽ�ֱ�Ϊ��
��ϵ�����㹫ʽ�ֱ�Ϊ�� ��
��![]() ������
������![]() ��
��![]() Ϊ������ֵ.
Ϊ������ֵ.
����Ŀ��Ϊ�˶�ij��������о����÷ֲ����������������У![]() ��
��![]() ��
��![]() �������Ա�У���ȡ����������о�С�飬�й����ݼ��±�����λ���ˣ�.
�������Ա�У���ȡ����������о�С�飬�й����ݼ��±�����λ���ˣ�.
��У | �����Ա | ��ȡ���� |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
��1����![]() ��
��![]() ��
��
��2�����Ӹ�У![]() ��
��![]() ��ȡ������ѡ2����ר�ⷢ�ԣ�����2�˶����Ը�У
��ȡ������ѡ2����ר�ⷢ�ԣ�����2�˶����Ը�У![]() �ĸ���.
�ĸ���.