[题目](1)已知P是矩形ABCD所在平面上的一点.则有.试证明该命题.(2)将上述命题推广到P为空间上任一点的情形.写出这个推广后的命题并加以证明.(3)将矩形ABCD进一步推广到长方体.并利用(2)得到的命题建立并证明一个新命题. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】（1）已知P是矩形ABCD所在平面上的一点，则有.试证明该命题.

（2）将上述命题推广到P为空间上任一点的情形，写出这个推广后的命题并加以证明.

（3）将矩形ABCD进一步推广到长方体，并利用（2）得到的命题建立并证明一个新命题.

【答案】（1）见解析（2）见解析（3）见解析

【解析】

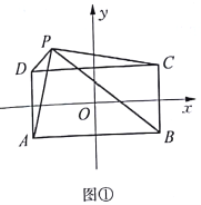
（1）如图①，设在直角坐标平面中，矩形ABCD的顶点坐标分别为，点是直角坐标平面上的任意一点，则

故.

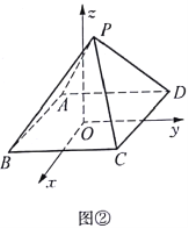
（2）推广命题：若棱锥P-ABCD的底面ABCD是矩形，则有.

证明：如图②，设棱锥的底面ABCD在空间直角坐标系的平面上，矩形ABCD的顶点坐标为，设P点坐标为，则

，

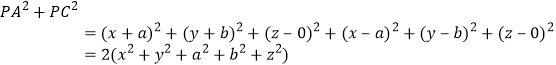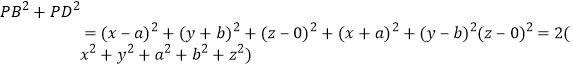故.

（3）再推广命题：设是长方体，P是空间上任意一点，则

证明：如图③，由（2）中定理可得

，

所以.

练习册系列答案

232 321 230 023 123 021 132 220 001

231 130 133 231 031 320 122 103 233

由此可以估计，恰好第三次就停止的概率为

A. B. C. D.

【题目】椭圆的右焦点为，左顶点为，线段的中点为，圆过点，且与交于，是等腰直角三角形，则圆的标准方程是____________

【题目】已知偶函数，当时，，若，为锐角三角形的两个内角，则（）

A. B.

C. D.

【题目】（1）已知圆过点，且与直线相切于点，求圆的方程；

（2）已知圆与轴相切，圆心在直线上，且圆被直线截得的弦长为，求圆的方程．

【题目】如果从北大打车到北京车站去接人，聪明的专家一定会选择走四环。虽然从城中间直穿过去看上去很诱人，但考虑到北京的道路几乎总是正南正北的方向，事实上不会真有人认为这样走能抄近路。在城市中，专家估算两点之间的距离时，不会直接去测量两点之间的直线距离，而会去考虑它们相距多少个街区。在理想模型中，假设每条道路都是水平或者竖直的，那么只要你朝着目标走（不故意绕远路），不管你这样走，花费的路程都是一样的。出租车几何学（taxicab geometry），所谓的“出租车几何学”是由十九世纪的另一位真专家赫尔曼-闵可夫斯基所创立的。在出租车几何学中，点还是形如的有序实数对，直线还是满足的所有组成的图形，角度大小的定义也和原来一样。只是直角坐标系内任意两点，定义它们之间的一种“距离”：，请解决以下问题：

（1）定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点的“距离”均为的“圆”方程，并作出大致图像；

（2）在出租车几何学中，到两点、“距离”相等的点的轨迹称为线段的“垂直平分线”，已知点，，；

①写出在线段的“垂直平分线”的轨迹方程，并写出大致图像；

②求证：三边的“垂直平分线”交于一点（该点称为的“外心”），并求出的“外心”.

【题目】杨辉三角，是二项式系数在三角形中的一种几何排列.在欧洲，这个表叫做帕斯卡三角形，帕斯卡（1623-1662）是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，这是我国数学史上的一个伟大成就.如图所示，在“杨辉三角”中，去除所有为1的项，依次构成数列，则此数列前135项的和为( )