题目内容
3.已知{an}{bn}是两个项数相同的等比数列,仿照表中的例子填写表格,从中你能得出什么结论?证明你的结论.| an | bn | an•bn | 判断{an•bn}是否是等比数列 | |
| 例 | 3×($\frac{2}{3}$)n | -5×2n-1 | -10×($\frac{4}{3}$)n-1 | 是 |
| 自选1 | ||||
| 自选2 |
分析 利用等比数列的通项与定义,即可得出结论.
解答 解:由题意,
| an | bn | an•bn | 判断{an•bn}是否是等比数列 | |
| 例 | 3×($\frac{2}{3}$)n | -5×2n-1 | -10×($\frac{4}{3}$)n-1 | 是 |
| 自选1 | 4×($\frac{2}{3}$)n | -5×4n-1 | -5×($\frac{8}{3}$)n | 是 |
| 自选2 | 3×($\frac{2}{3}$)n | 5×2n-1 | 10×($\frac{4}{3}$)n-1 | 是 |
证明:令an=a1qn-1,bn=b1q′n-1,∴an•bn=a1qn-1b1q′n-1=(a1b1)(qq′)n-1,
∴{an•bn}是等比数列.
点评 本题考查等比数列的通项与定义,考查学生 的计算能力,比较基础.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.集合A={x|x≥1},B={x|x<m},若A∪B=R,则m的最小值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
11.设有3个点(x1,y1),(x2,y2),(x3,y3),由最小二乘法来刻画直线y=a+bx与这3个点的接近程度时,其表达式是( )
| A. | |x1-(a+bx1)|+|x2-(a+bx2)|+|x3-(a+bx3)| | B. | [x1-(a+bx1)]2+[x2-(a+bx2)]2+[x3-(a+bx3)]2 | ||
| C. | |y1-(a+bx1)|+|y2-(a+bx2)|+|y3-(a+bx3)| | D. | [y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2 |
20.正四面体A-BCD的顶点都在一个球面上,E,F分别是AB,BC的中点,直线EF被球面所截得的线段长为$\sqrt{15}$,则该球的表面积为( )
| A. | 21π | B. | 18π | C. | 12π | D. | 9π |
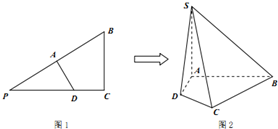 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.