题目内容
9.椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1上的点到左准线的距离为5,那么它到右焦点的距离为( )| A. | $\frac{25}{4}$ | B. | $\frac{15}{2}$ | C. | 4 | D. | 6 |
分析 求出椭圆的a,b,c,e,分别运用椭圆的第二定义,求得点到左焦点的距离,再由第一定义,即可得到所求距离.
解答 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的a=5,b=3,c=$\sqrt{{a}^{2}-{b}^{2}}$=4,
e=$\frac{c}{a}$=$\frac{4}{5}$,
设点到左焦点的距离为d,点到右焦点的距离为k,
利用椭圆的第二定义:$\frac{d}{5}$=e=$\frac{4}{5}$,
解得d=4,
再由椭圆的第一定义:d+k=10,
解得:k=6,
故选D.
点评 本题考查的知识要点:椭圆的离心率的应用,椭圆的第一、第二定义的应用.定义法解题是处理圆锥曲线问题中常用方法,要掌握.

练习册系列答案
相关题目
11.设有3个点(x1,y1),(x2,y2),(x3,y3),由最小二乘法来刻画直线y=a+bx与这3个点的接近程度时,其表达式是( )
| A. | |x1-(a+bx1)|+|x2-(a+bx2)|+|x3-(a+bx3)| | B. | [x1-(a+bx1)]2+[x2-(a+bx2)]2+[x3-(a+bx3)]2 | ||
| C. | |y1-(a+bx1)|+|y2-(a+bx2)|+|y3-(a+bx3)| | D. | [y1-(a+bx1)]2+[y2-(a+bx2)]2+[y3-(a+bx3)]2 |
20.正四面体A-BCD的顶点都在一个球面上,E,F分别是AB,BC的中点,直线EF被球面所截得的线段长为$\sqrt{15}$,则该球的表面积为( )
| A. | 21π | B. | 18π | C. | 12π | D. | 9π |
4.已知函数f(x)=x3-3x2+a,若f(x+1)是奇函数,则曲线y=f(x)在点(0,a)处的切线方程是( )
| A. | x=0 | B. | x=2 | C. | y=2 | D. | y=4 |
14.某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取M名同学的成绩,数据的分组统计表如下:
(1)求出表中M,n的值;
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004 |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.38 | 0.038 |
| (80,90] | m | n | p |
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 | M | N | P |
(2)为了了解某些同学在数学学习中存在的问题,现从样本中分数在(40,60]中的6位同学中任意抽取2人进行调查,求分数在(40,50]和(50,60]中各有一人的概率.
18.为了考查培育的某种植物的生长情况,从试验田中随机抽取50株该植物进行检测,得到该植物高度的频数分布表如下:
(Ⅰ)写出表中①②③④处的数据;
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
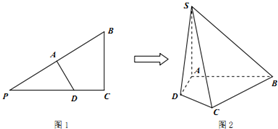 如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.
如图1,在△PBC中,∠C=90°,PC=4,BC=3,PD:DC=5:3,AD⊥PB,将△PAD沿AD边折起到SAD位置,如图2,且使SB=$\sqrt{13}$.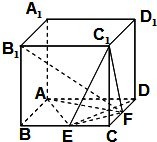 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,