题目内容
【题目】在极坐标系中,曲线C1:ρsin2θ=4cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C2的参数方程为: ![]() ,(θ∈[﹣
,(θ∈[﹣ ![]() ,
, ![]() ]),曲线C:
]),曲线C:  (t为参数).
(t为参数).
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)C与C1相交于A,B,与C2相切于点Q,求|AQ|﹣|BQ|的值.
【答案】解:(Ⅰ)∵x=ρcosθ,y=ρsinθ, 由ρsin2θ=4cosθ,得ρ2sin2θ=4ρcosθ,
∴曲线C1的直角坐标方程为:y2=4x.
(Ⅱ)设Q(cosθ,sinθ),(θ∈[﹣ ![]() ,
, ![]() ]),由题意知直线C的斜率k=
]),由题意知直线C的斜率k= ![]() ,
,
所以 ![]() ,即
,即 ![]() =tanθ=﹣
=tanθ=﹣ ![]() ,
,
所以 ![]() ,故Q(
,故Q( ![]() ,﹣
,﹣ ![]() ).
).
取 ![]() ,
, ![]() ,不妨设A,B对应的参数分别为t1 , t2 .
,不妨设A,B对应的参数分别为t1 , t2 .
把 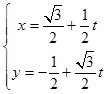 ,代入y2=4x,
,代入y2=4x,
化简得 ![]() ,即3t2﹣(8+2
,即3t2﹣(8+2 ![]() )t﹣8
)t﹣8 ![]() =0,
=0,
∵C与C1相交于A,B,∴△>0,t1+t2= ![]() .
.
∴|AQ|﹣|BQ|=|t1+t2|= ![]()
【解析】(Ⅰ)由x=ρcosθ,y=ρsinθ,能求出曲线C1的直角坐标方程.(Ⅱ)设Q(cosθ,sinθ),(θ∈[﹣ ![]() ,
, ![]() ]),由题意知直线C的斜率k=
]),由题意知直线C的斜率k= ![]() ,从而
,从而 ![]() =tanθ=﹣
=tanθ=﹣ ![]() ,进而Q(
,进而Q( ![]() ,﹣
,﹣ ![]() ).设A,B对应的参数分别为t1 , t2 . 把
).设A,B对应的参数分别为t1 , t2 . 把 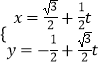 ,代入y2=4x,得3t2﹣(8+2
,代入y2=4x,得3t2﹣(8+2 ![]() )t﹣8
)t﹣8 ![]() =0,由此利用韦达定理能求出|AQ|﹣|BQ|.
=0,由此利用韦达定理能求出|AQ|﹣|BQ|.

练习册系列答案
相关题目


