题目内容
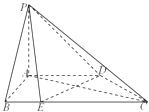
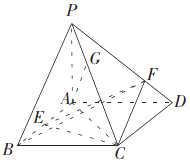
【题目】已知四棱锥P﹣ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2 ![]() ,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上. 
(Ⅰ)证明:CD⊥AG;
(Ⅱ)若三棱锥E﹣BCF的体积为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)证明:依题意,因为AB∥CD,AC⊥BA,所以AC⊥CD. 又因为PA⊥底面ABCD,所以PA⊥CD,
因为AC∩PA=A,所以CD⊥平面PAC,
因为AG平面PAC,所以CD⊥AG.
(Ⅱ)解:设点F到平面ABCD的距离为d,
则 ![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
故 ![]() .
.
【解析】(Ⅰ)由AB∥CD,AC⊥BA,可得AC⊥CD.由PA⊥底面ABCD,可得PA⊥CD,可得CD⊥平面PAC,即可证明CD⊥AG.(II)设点F到平面ABCD的距离为d,利用三棱锥的体积计算公式可得:VE﹣BCF=VF﹣BEC , 可得d,进而得出答案.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目